センター2019物理第５問「熱サイクルとp-Tグラフ」

スポンサーリンク

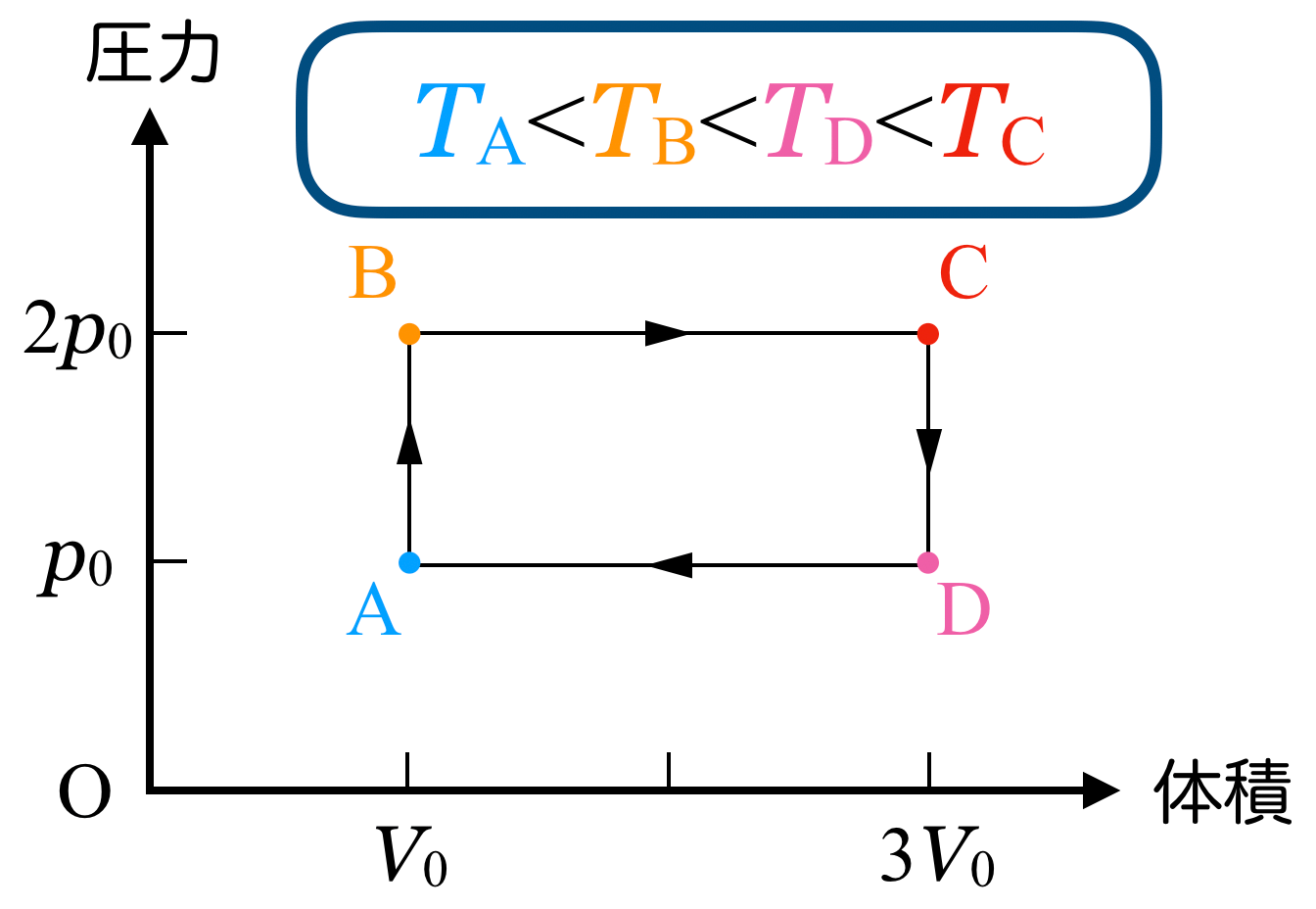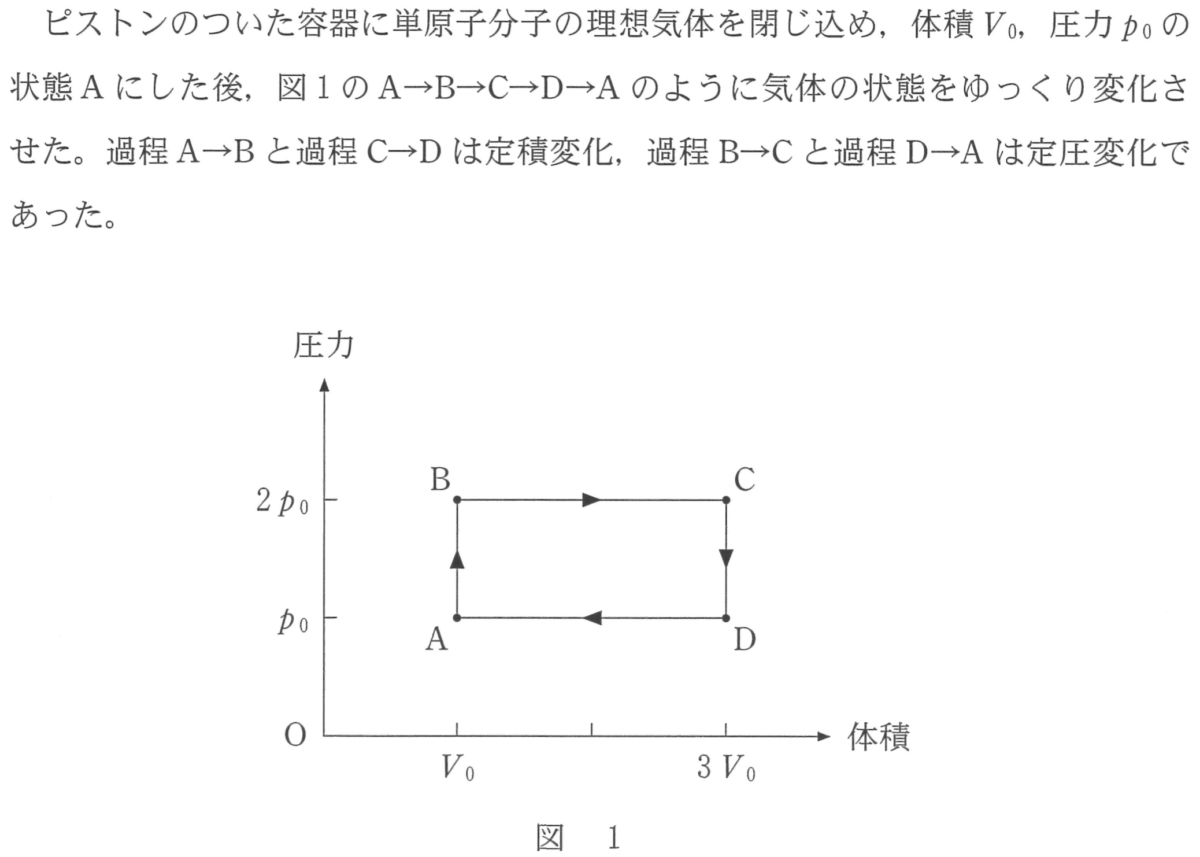
温度の関係を求めておこう

物理が得意な秀樹
今日は時間がないから，各点での温度を出しておこうか。各点の温度をそれぞれ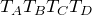T_A，T_B，T_C，T_Dとしておこう。
物理が苦手な文子
ボイル・シャルルの法則ね。

    \begin{eqnarray*}\frac{p_0V_0}{T_A}=\frac{2p_0V_0}{T_B}=\frac{2p_0\cdot 3V_0}{T_C}=\frac{p_0\cdot 3V_0}{T_D}\end{eqnarray*}

よって，

    \begin{eqnarray*}T_B&=&2T_A\\T_C&=&6T_A\\T_D&=&3T_A\end{eqnarray*}

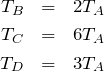
物理が得意な秀樹
いいね。これで温度の関係が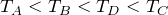T_A<T_B<T_D<T_Cということが分かったね。それじゃあ，過程A→Bを考えよう。体積が変わらない定積変化だね。
物理が苦手な文子
ということは外部にする仕事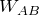W_{AB}は0ね。
物理が得意な秀樹
A→Bで温度は上昇しているから，内部エネルギーは増加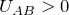（\Dlta U_{AB}>0）しているよね。
物理が苦手な文子
つまり，熱力学第一法則を考えると，外部から吸収した熱量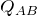Q_{AB}は，

    $$Q_{AB}=\Dlta U_{AB}+W_{AB}>0$$

となるから，外部から熱を吸収しているわね。
物理が得意な秀樹
まとめると，気体が熱を「外部から吸収」し，気体の内部エネルギーは「増加する」ということで，答えは①だ。

仕事の総和は囲まれた部分の面積

物理が苦手な文子
「外部にした仕事の総和」ってどういうこと？
物理が得意な秀樹
外部にした仕事を正，外部からされた仕事を負として総和を求めなさいということだね。ちょっとわかりにくい表現だという意見もあるけどね。
物理が苦手な文子
確か，仕事はp-Vグラフの面積で求めることができるのよね。
物理が得意な秀樹
その通り。求めてみよう。
物理が苦手な文子
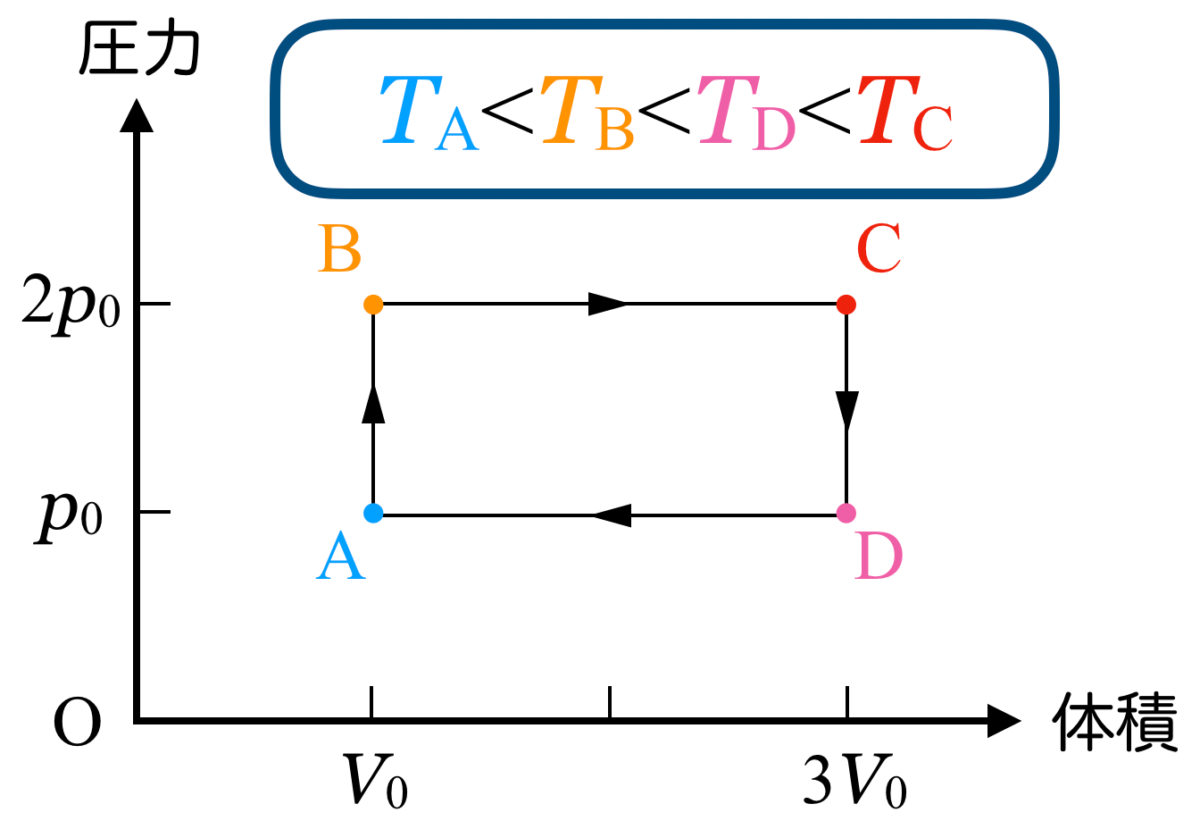
気体の体積が変わっていない過程A→Bと過程C→Dの仕事は0ね。体積が増えている過程B→Cは外部にした仕事は正ね。この面積を求めればいいわね。
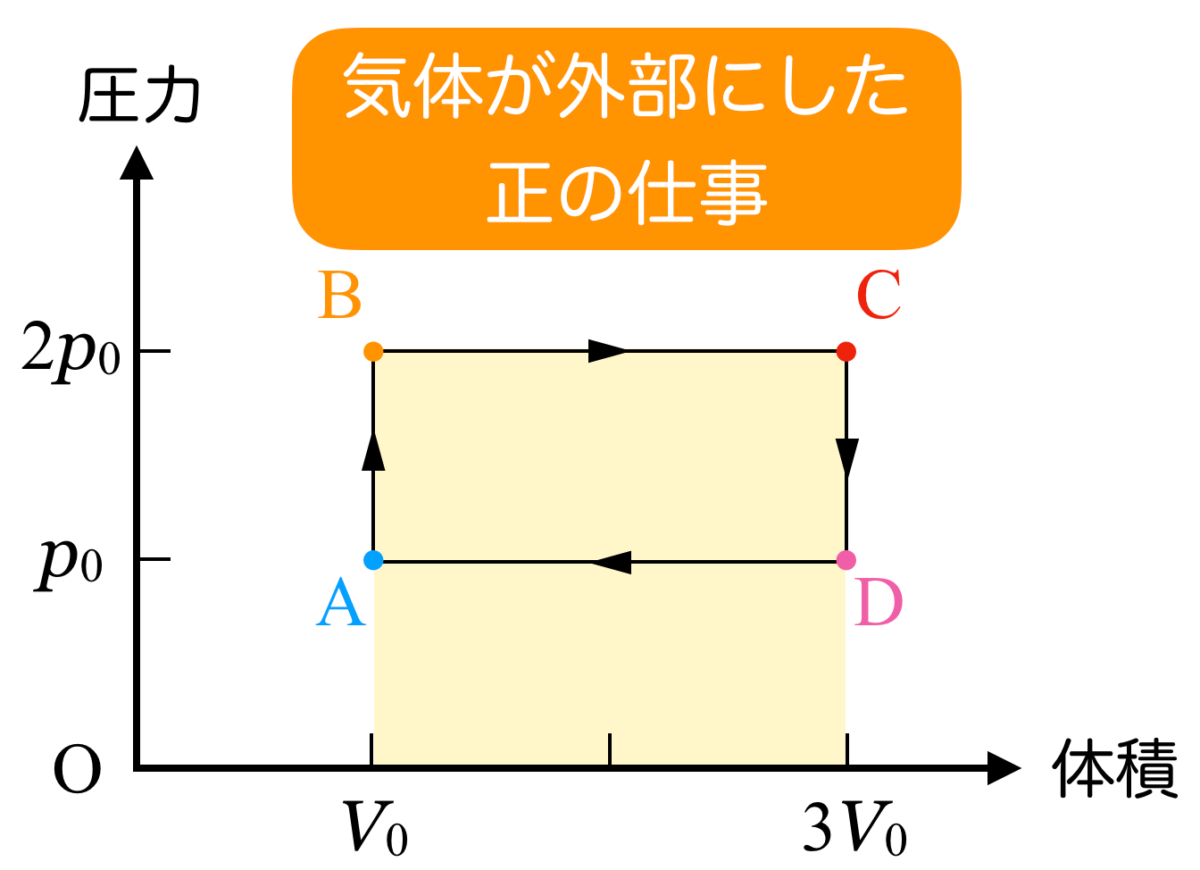
物理が得意な秀樹
面積を求める前に，過程D→Aも考えちゃおう。
物理が苦手な文子
過程D→Aは体積が減っているから負の仕事をしたのね。
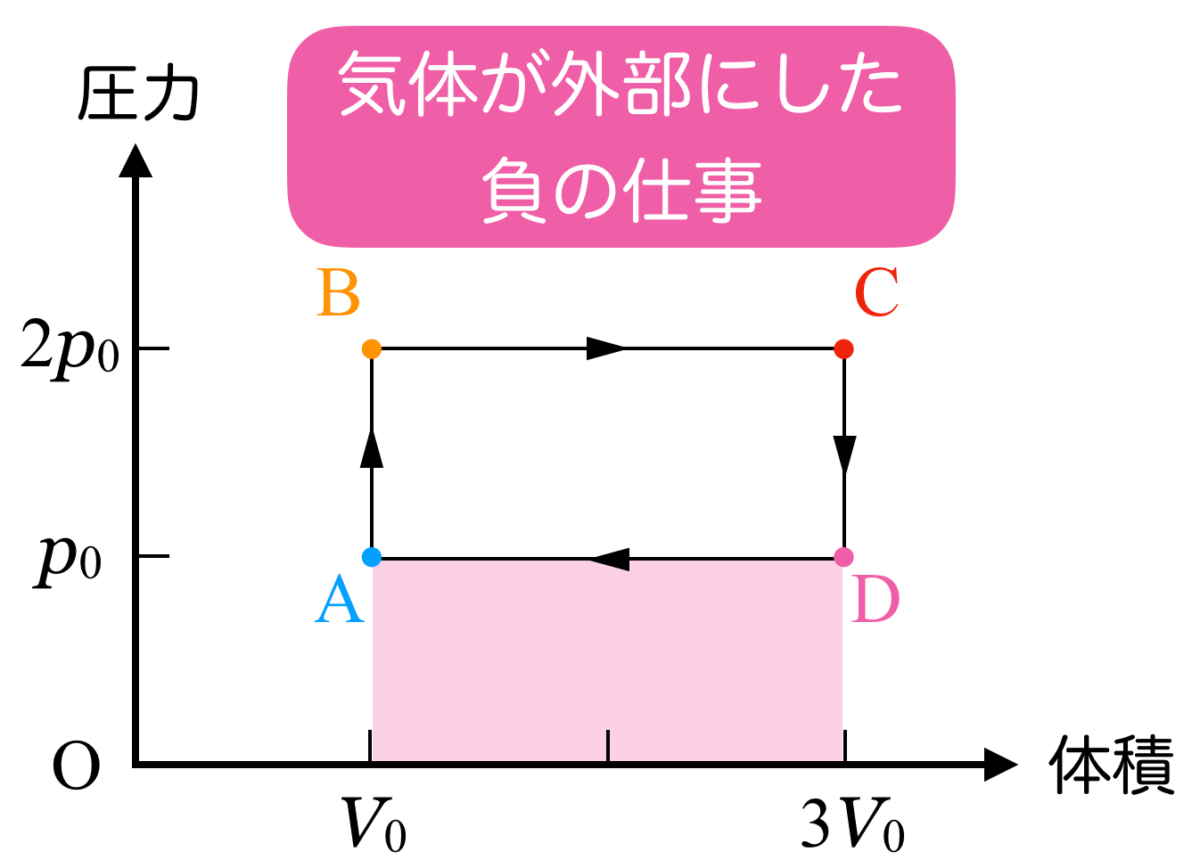
物理が得意な秀樹
ということは，面積を引き算したABCDで囲まれる部分の面積が，求める「外部にした仕事の総和」になるね。
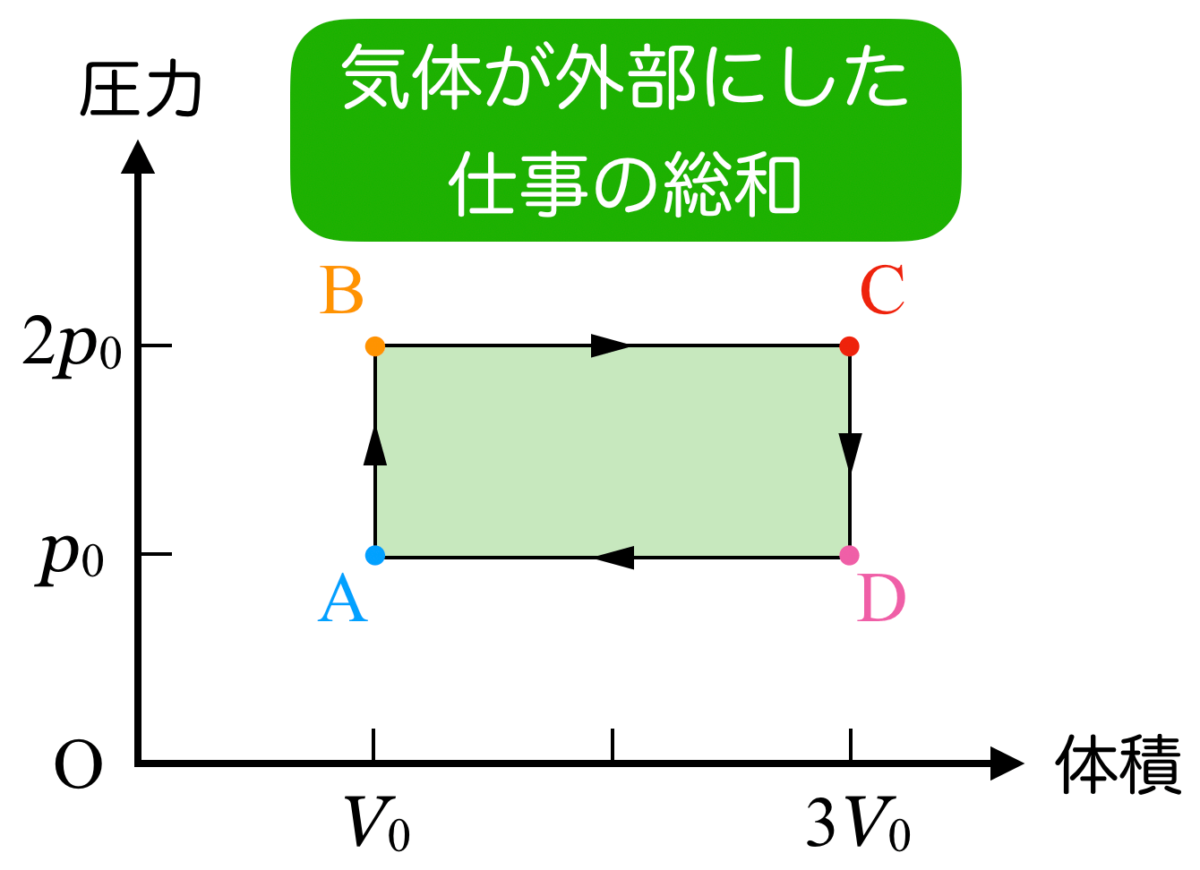
物理が苦手な文子
単純に長方形の面積を計算すればいいのよね。

    \begin{eqnarray*}W&=&(2p_0-p_0)(3V_0-V_0)\\&=&2p_0V_0\end{eqnarray*}

物理が得意な秀樹
そうだね。答えは③だ。

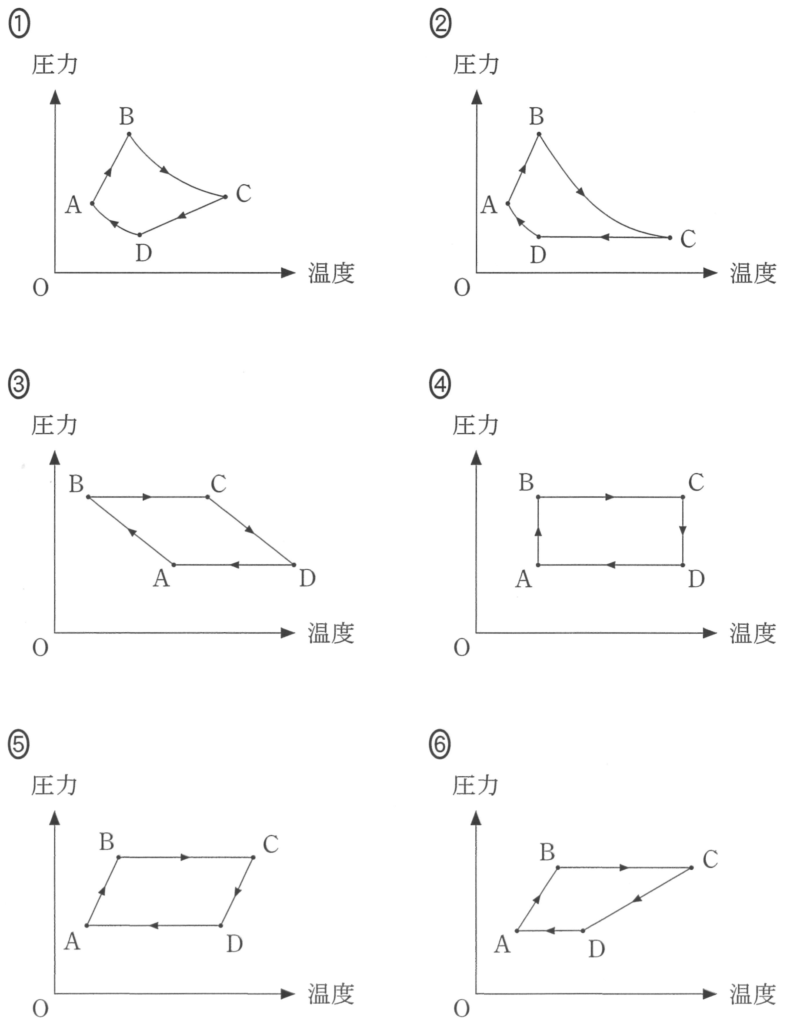
ここでも温度の関係が役に立つ

物理が苦手な文子
最初に温度を求めたから，これは簡単ね。
物理が得意な秀樹
そうだね。まず，過程B→Cと過程D→Aは定圧変化だから，①と②は違うね。DよりもCの方が温度が高いから，⑤か⑥のどちらかだ。
物理が苦手な文子
最初に求めた温度の比と合っているのは⑥ね。
物理が得意な秀樹
そうだね。あとは定積変化のときは，圧力と温度は比例関係になるから，原点を通る直線じゃなきゃだめだよね。やっぱり⑥が答えだ。
タイトルとURLをコピーしました