センター2019物理追試第２問Ｂ「直線電流が作る磁場から受ける力と電磁誘導」

スポンサーリンク

いろいろな公式が出てくるので，確認しよう

物理が苦手な文子
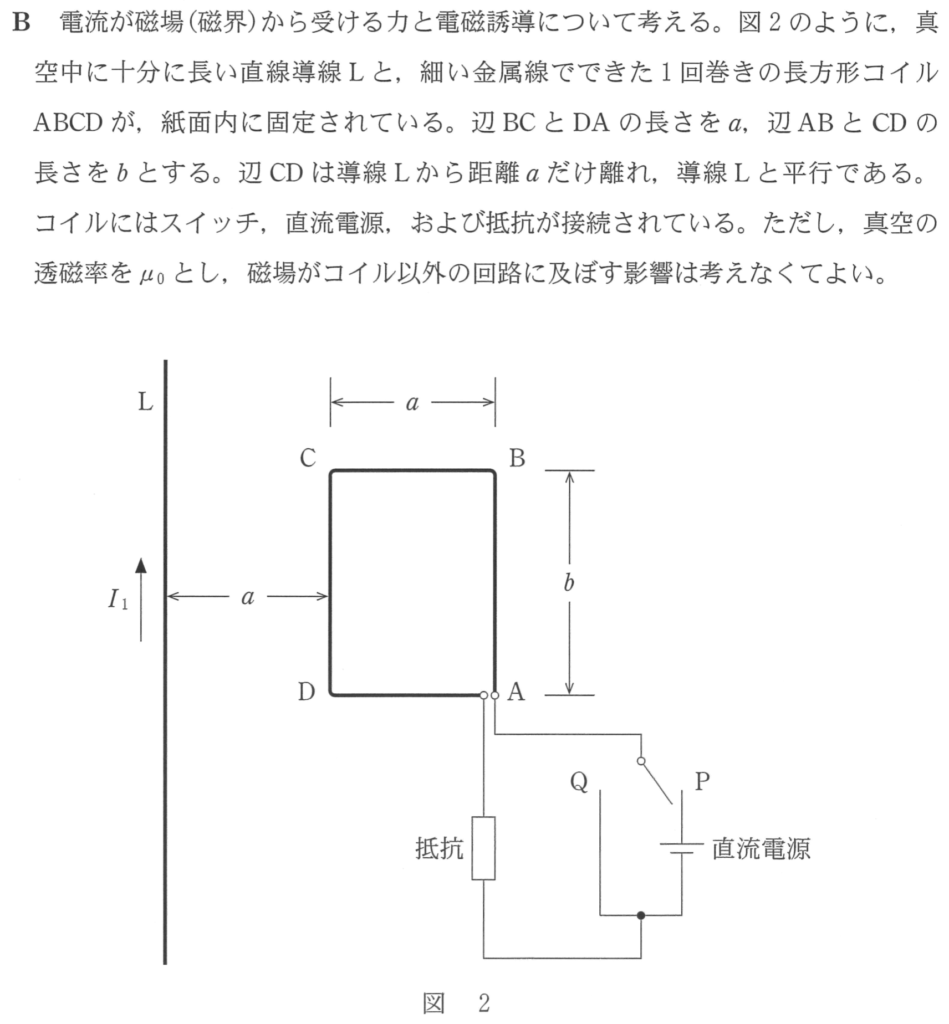
導線Lには電流が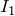I_1流れていて，コイルには電流が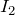I_2流れているのね。
物理が得意な秀樹
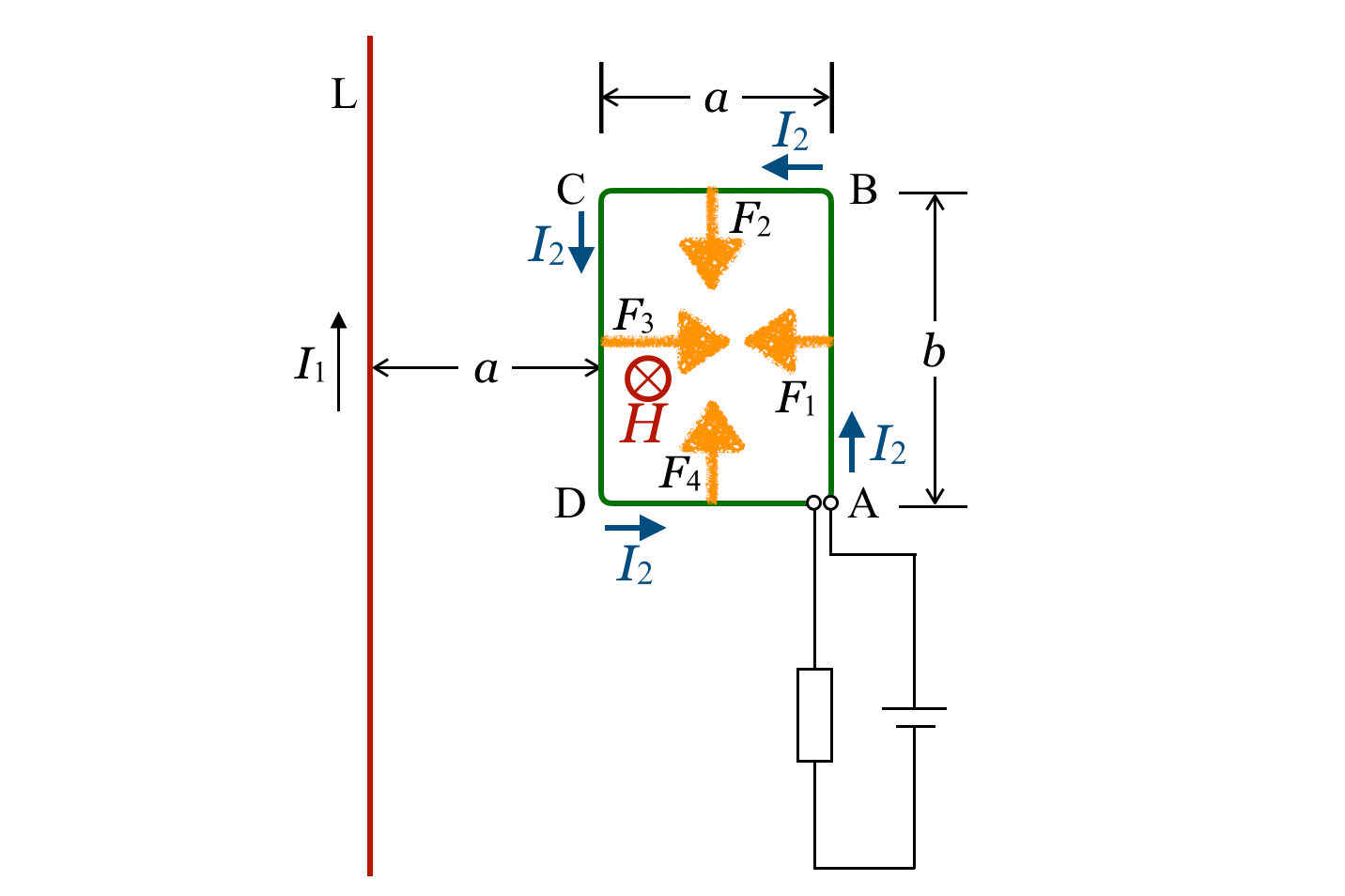
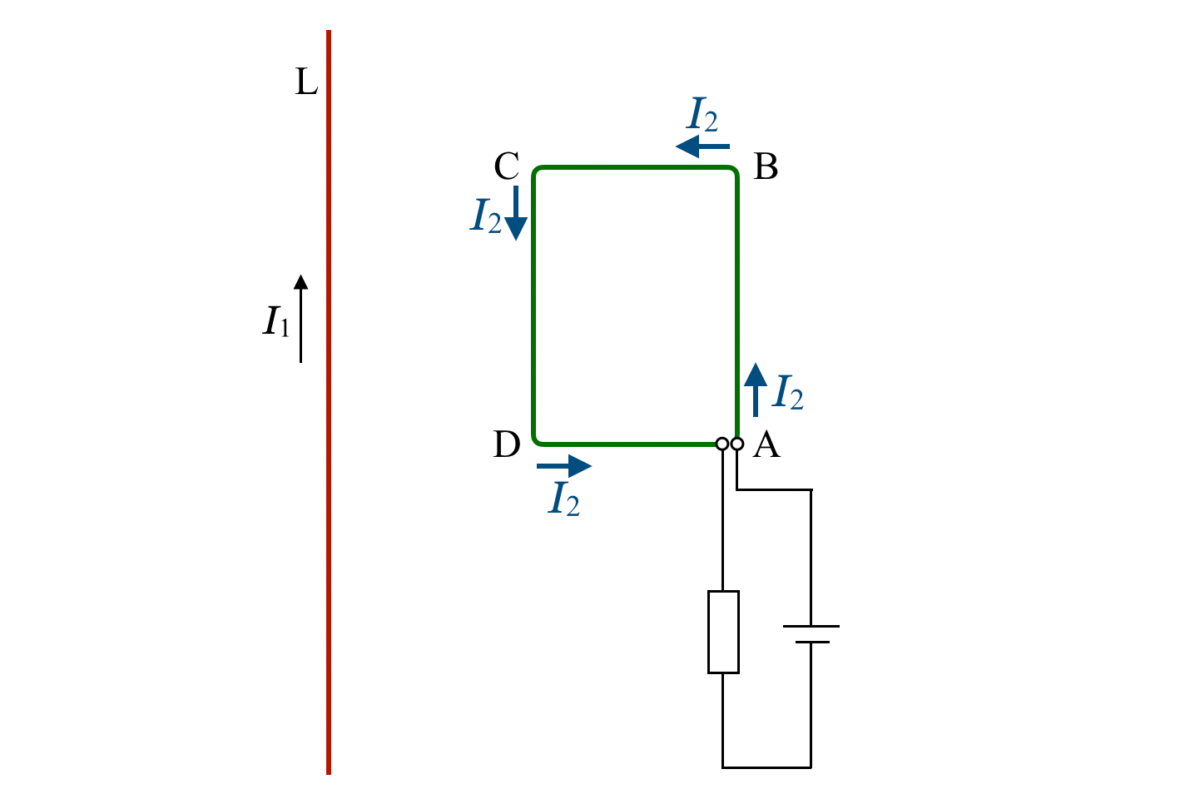
導線Lを流れる電流は，コイルのある側（導線の右側）に紙面に垂直に表から裏の向きの磁場を作るよね。
物理が苦手な文子
向きは右ねじの法則で求められるのよね。そうすると，電流は磁場から力を受けるわね。力の向きはフレミング左手の法則で考えて，すべてコイルの内側を向くわ。
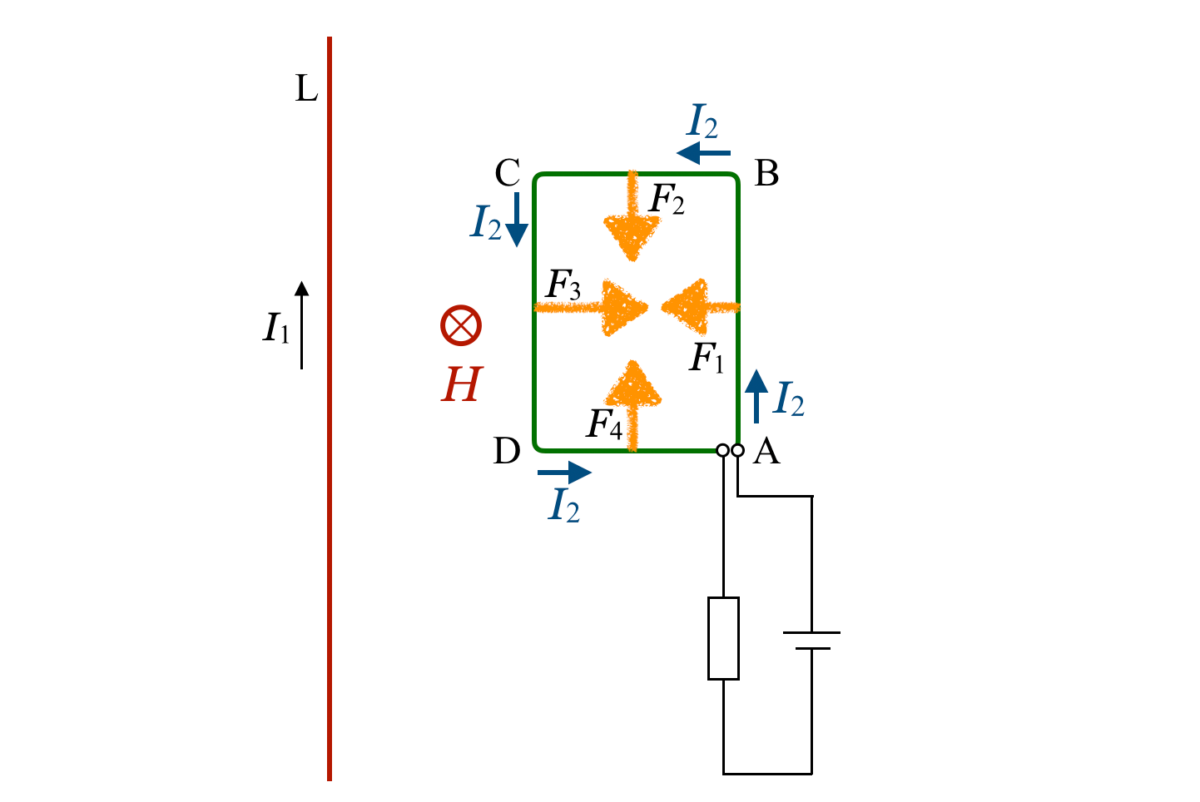
物理が得意な秀樹
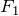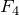４辺にはたらく力にF_1からF_4まで図のように名前をつけて，その大きさを考えよう。
物理が苦手な文子
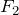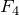この中で，辺BCにはたらく力と辺DAにはたらく力は場所によって違うけど，それぞれの合力F_2とF_4は，同じ大きさで逆向きだから力がつり合っているのね。
物理が得意な秀樹
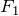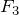そういうことだね。残りのF_1とF_3の大きさを求めるために，図に辺の長さなども書き加えると，ごちゃごちゃしちゃうけど，こんな感じね。
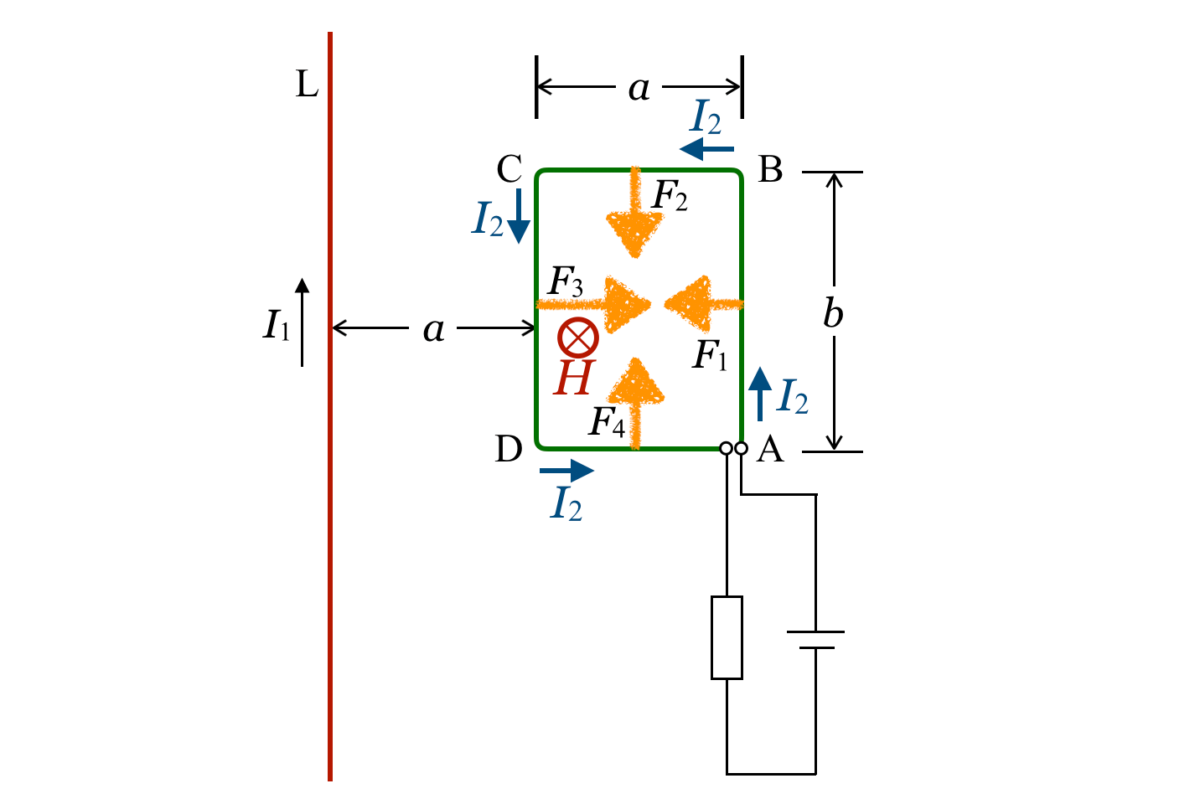
物理が得意な秀樹
次に公式の確認だけど，直線電流が作る磁場はこうだよ。
物理が苦手な文子
曲線電流からの距離rに反比例するのよね。だから，辺ABと辺CDでは直線電流に近い辺CDの場所の方が電場は強いということになるわね。

    \begin{eqnarray*}H_{AB}&=&\frac{I_1}{2\pi \cdot 2a}\\H_{CD}&=&\frac{I_1}{2\pi a}\end{eqnarray*}

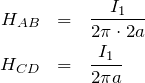
物理が得意な秀樹
次に，磁束密度の磁場の関係はこうだ。
物理が苦手な文子
力の大きさはこうね。
物理が苦手な文子
まとめると，

    \begin{eqnarray*}F_1&=&I_2\cdot \mu_0\cdot \frac{I_1}{4\pi a}\cdot b\\F_3&=&I_2\cdot \mu_0\cdot \frac{I_1}{2\pi a}\cdot b\end{eqnarray*}

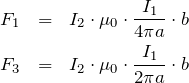
物理が得意な秀樹
その２力の合力は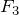，F_3の方が大きいから右向きだね。
物理が苦手な文子
合力の大きさ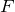Fは，

    \begin{eqnarray*}F&=&F_3-F_1\\&=&\frac{\mu_0 I_1 I_2 b}{2\pi a}-\frac{\mu_0 I_1 I_2 b}{4\pi a}\\&=&\frac{\mu_0 I_1 I_2 b}{4\pi a}\end{eqnarray*}

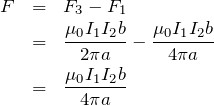
物理が得意な秀樹
合ってるよ。空欄３の答えは①で，空欄４の答えは④だ。

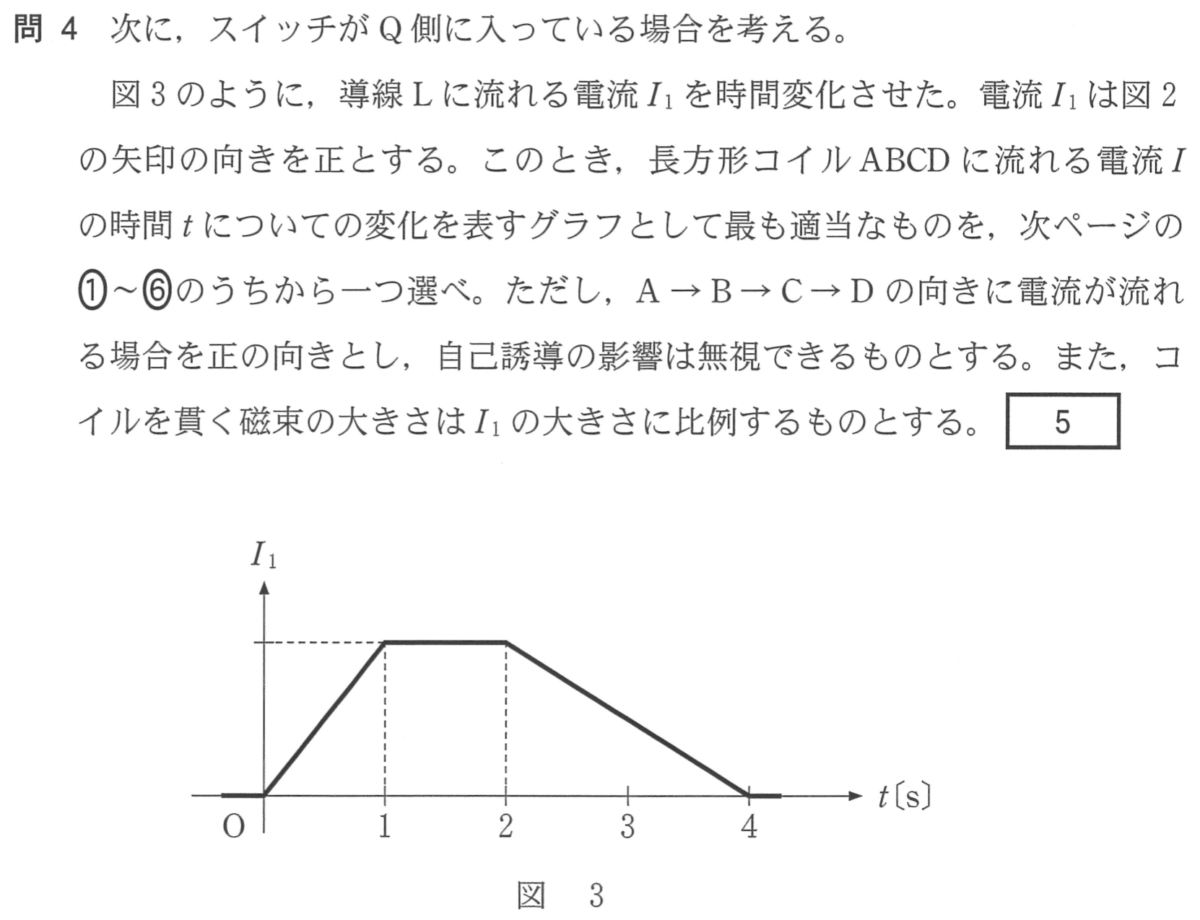
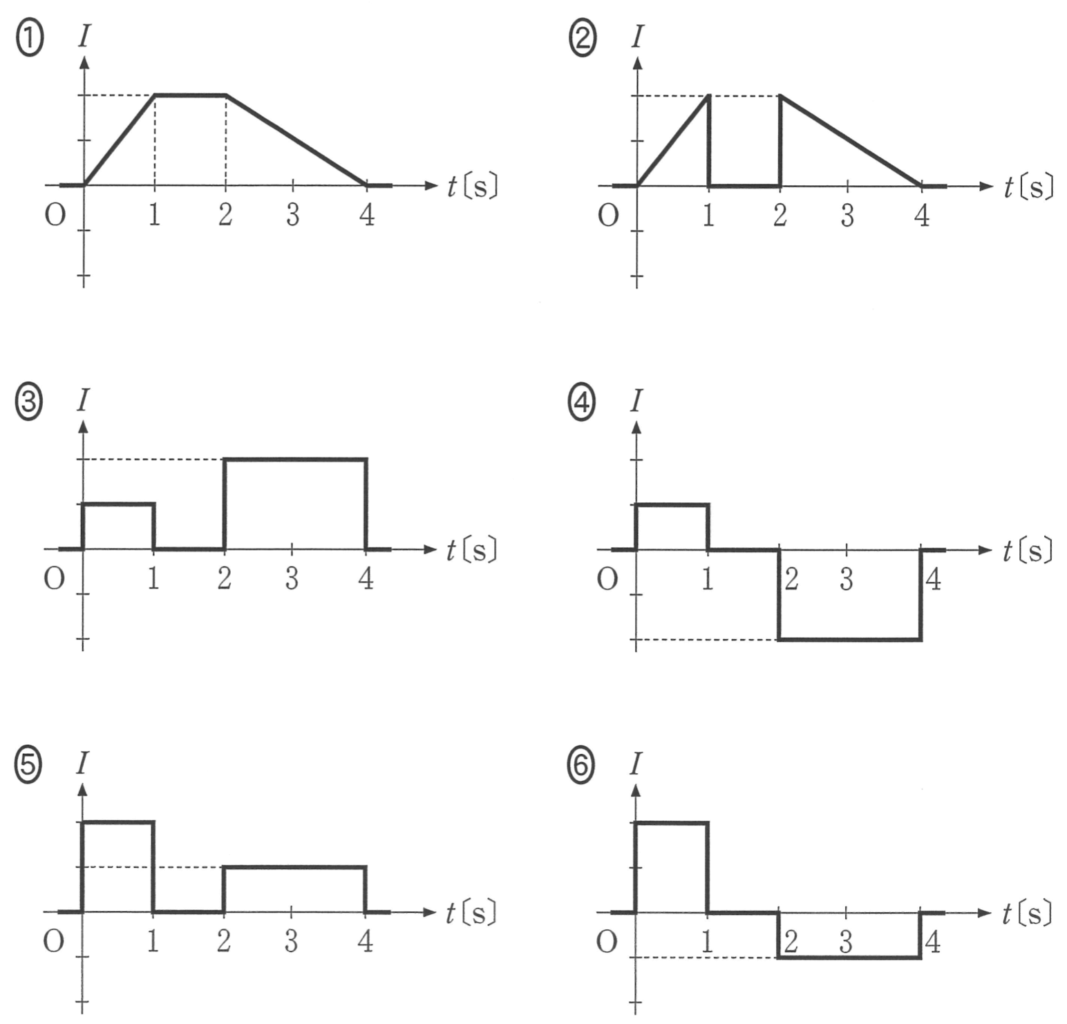
指定された正の向きを確認する

物理が苦手な文子
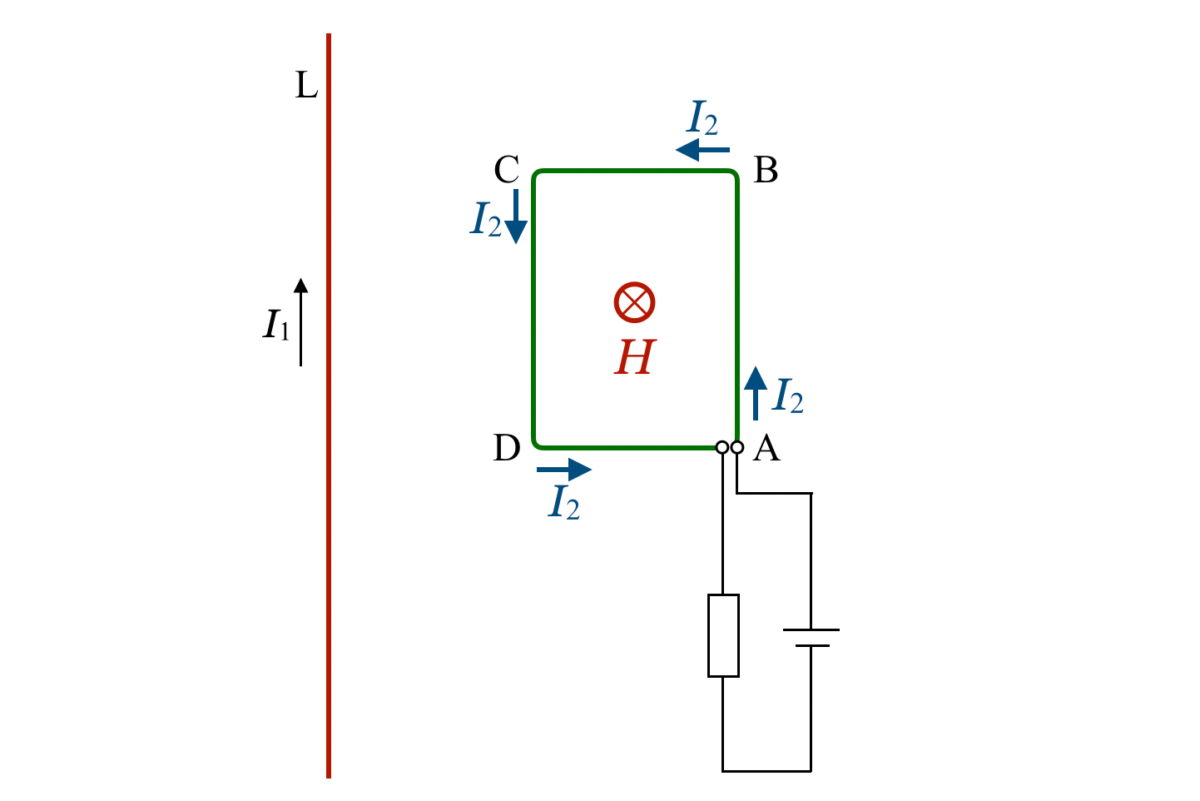
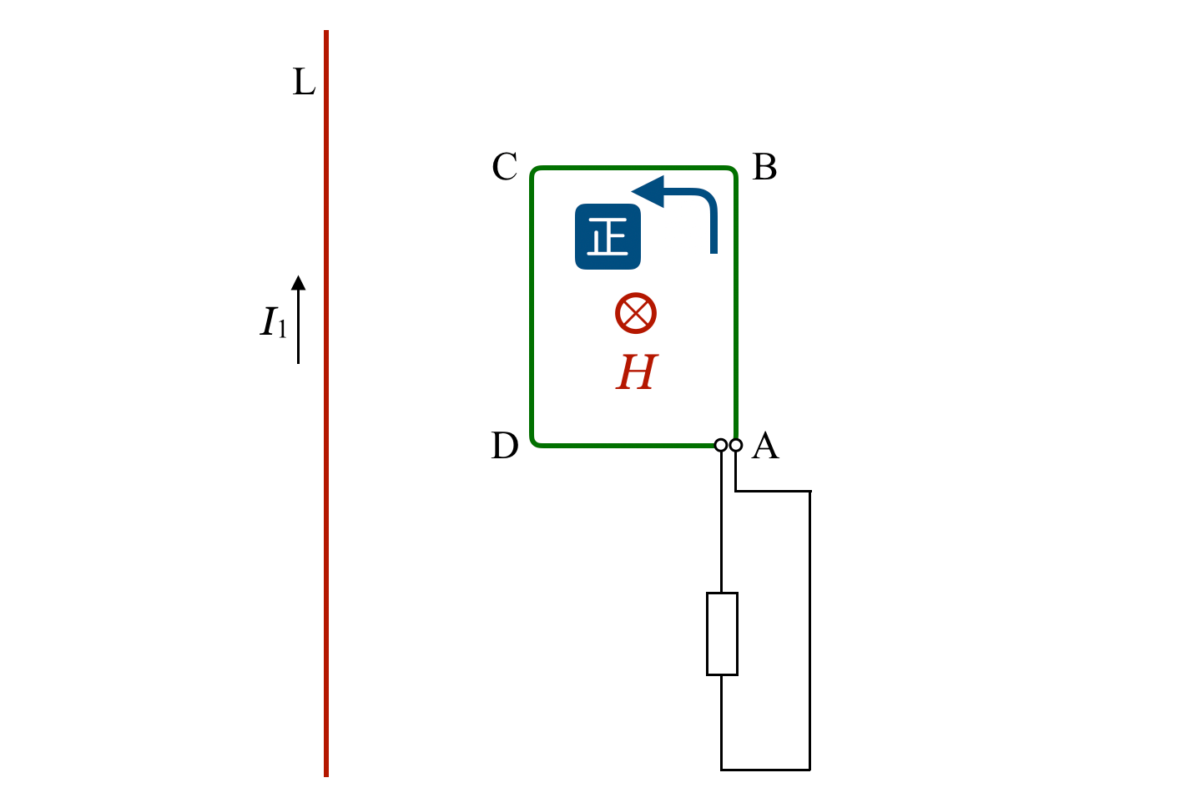
電流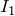I_1が変化すると，コイルの周りの磁場が変化するわよね。
物理が得意な秀樹
コイルを貫く磁束が変化するとコイルに誘導起電力が生じるね。
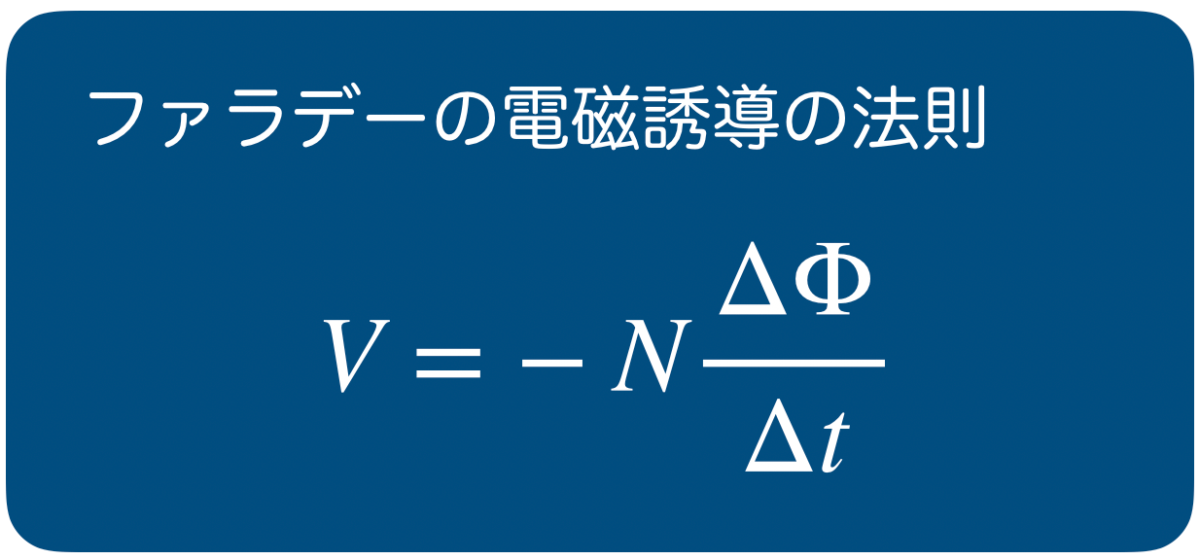
物理が苦手な文子
この問題では大きさは求める必要がなくて，向きと大小関係が分かれば良さそうね。
物理が得意な秀樹
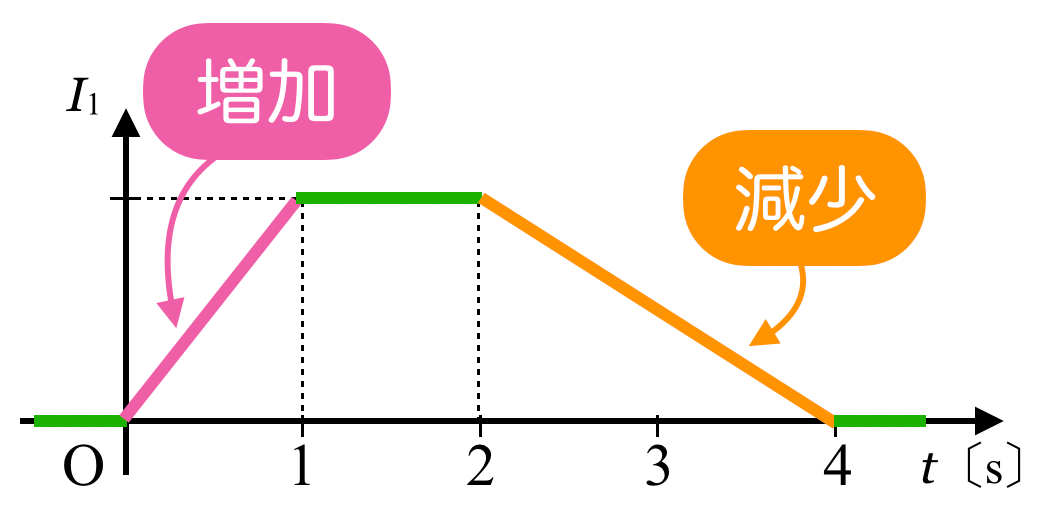
グラフと，指定された正の向きを確認するよ。
物理が苦手な文子
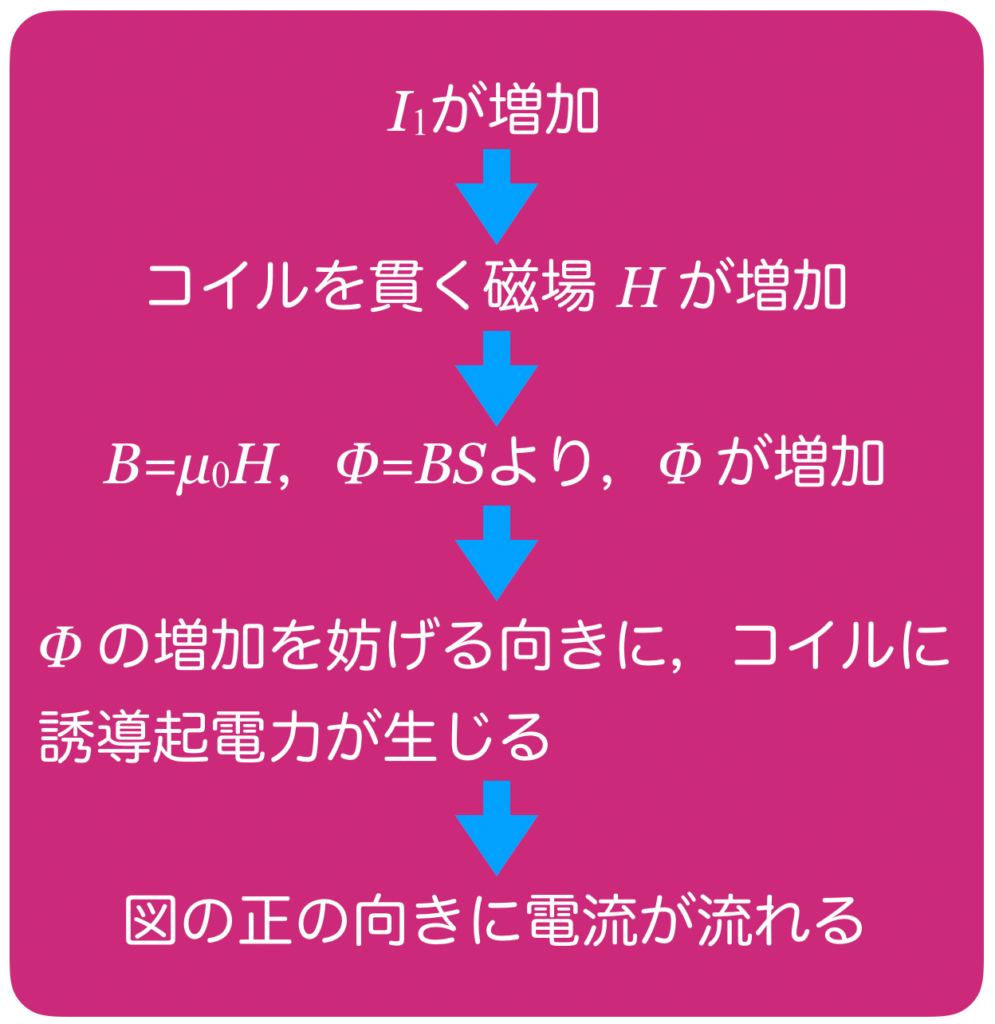
順番に考えると，こんな感じね。
物理が得意な秀樹
ということは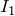，I_1が増加している0〜1sのときにコイルを流れる電流は正で，減少している2〜4sのときは負になるね。選択肢は④と⑥に絞られるけど，どっちにする？
物理が苦手な文子
0〜1sは1s間で増加しているけど，2〜4sは同じ電流の差を2s間で減少しているから，起電力の大きさが大きいのは0〜1sね。
物理が得意な秀樹
その通り！答えは⑥だ。
タイトルとURLをコピーしました