センター2019物理追試第４問Ｂ「天井がある空間における斜方投射」

スポンサーリンク

鉛直方向を考えて落下までの時間を求める

物理が苦手な文子
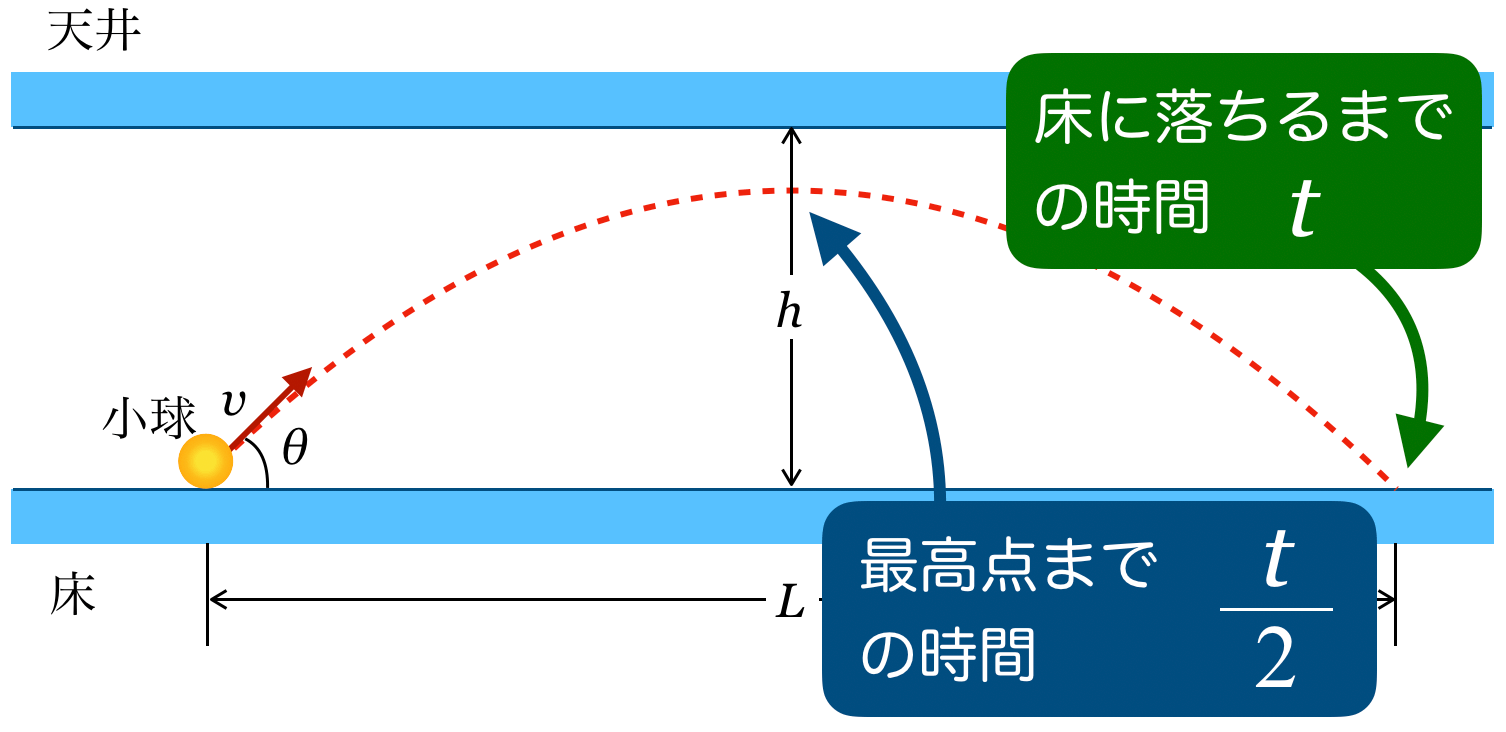
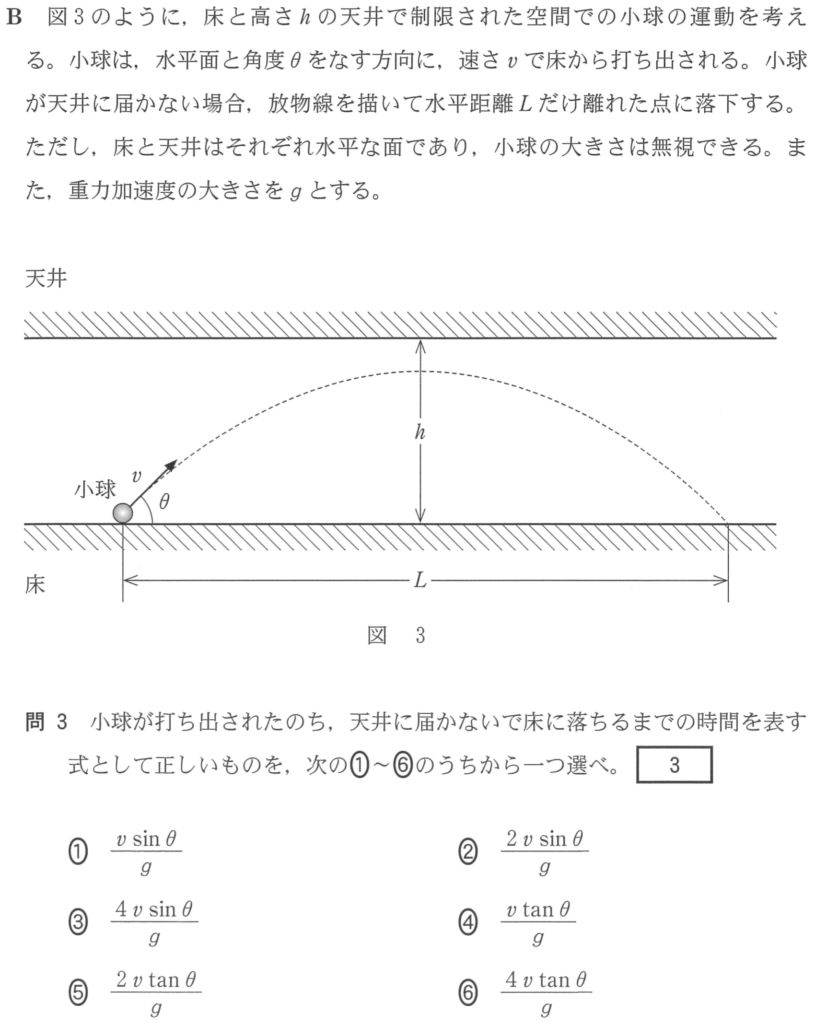
斜方投射の問題だけど，天井があるのね。ちょっと邪魔だわ。
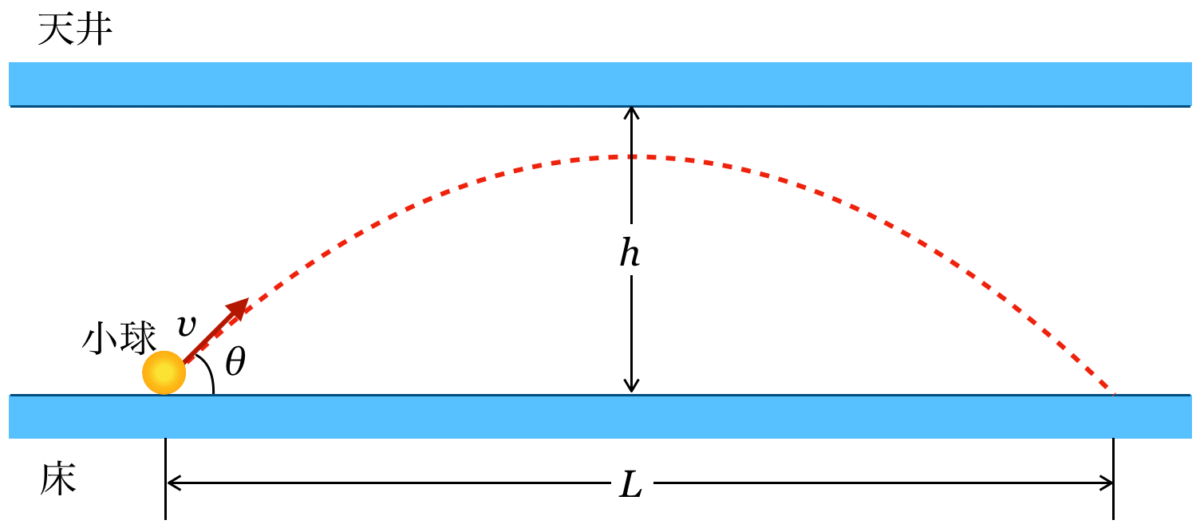
物理が得意な秀樹
最初の問いでは天井には届かないので，気にせずに問いて大丈夫だよ。
物理が苦手な文子
それじゃあ，まずは初速度を分けるわね。
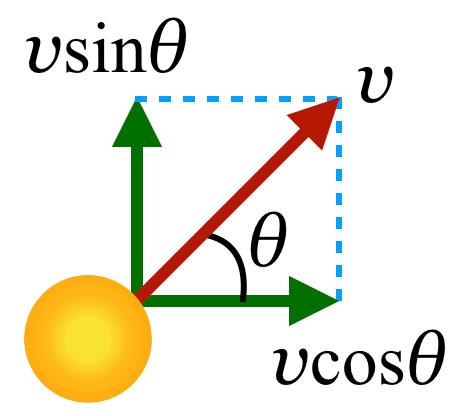
物理が得意な秀樹
床に落ちるまでの時間を求めるので，等加速度直線運動の

    $$x=v_0t+\frac{1}{2}at^2$$

を使えばいいね。
物理が苦手な文子
鉛直方向で考えると，

    $$0=v\sin\theta \cdot t+\frac{1}{2}(-g)t^2$$

となって，t≠0だから，

    $$t=\frac{2v\sin\theta}{g}$$

物理が得意な秀樹
そうだね。答えは②だ。

最高点までの時間は，落下時間の半分

物理が苦手な文子
まずは天井に届かない条件ね。
物理が得意な秀樹
いくつかやり方はあるけど，前の問いで落下までの時間を求めたから，それを使おうか。
物理が苦手な文子
落下までの時間を使って，天井に届かない条件を求めるの？
物理が得意な秀樹
落下までの時間が分かったら，最高点までの時間が分かるよね。
物理が苦手な文子
そういうことね。最高点までの時間は，落下までの時間の半分ね。

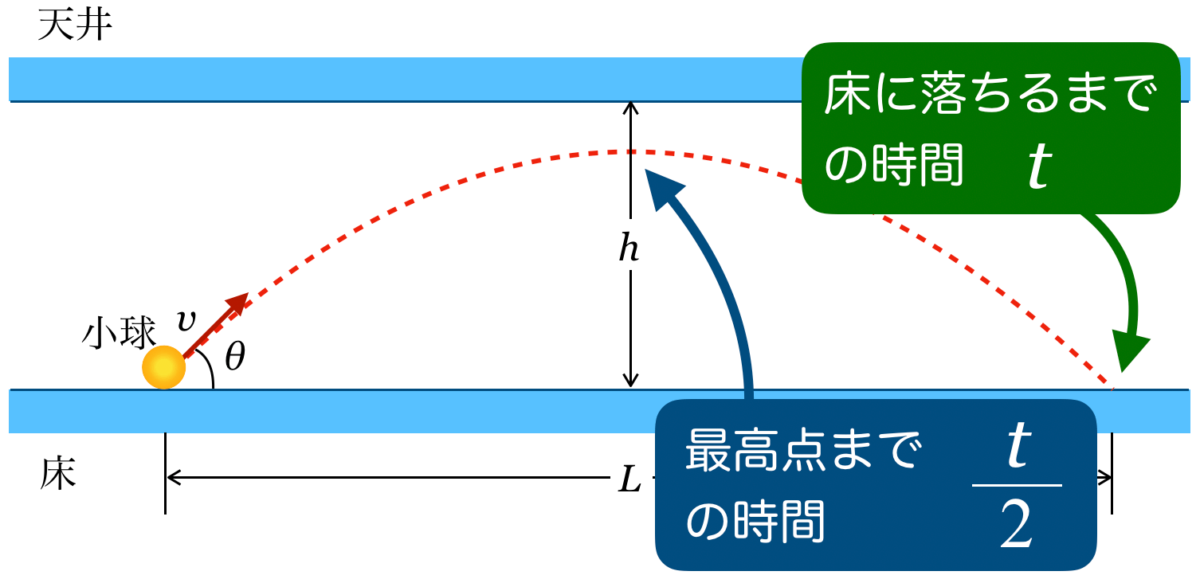
最高点y<hという不等式を立てる

物理が得意な秀樹
最高点の高さを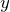yとして求めてみようか。
物理が苦手な文子
使うのはさっきと同じ式ね。

    \begin{eqnarray*}y&=&v\sin\theta\cdot\frac{v\sin\theta}{g}-\frac{g}{2}\cdot\left(\frac{v\sin\theta}{g}\right)^2\\&=&\frac{v^2\sin^2\theta}{2g}\end{eqnarray*}

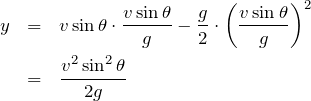
物理が得意な秀樹
いいね。この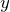yが天井の高さ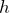hより低ければいいんだよね。
物理が苦手な文子
つまり，

    \begin{eqnarray*}\frac{v^2\sin^2\theta}{2g}&<&h\\v^2\sin^2\theta&<&2gh\end{eqnarray*}

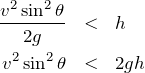
物理が得意な秀樹
それでいいね。これで答えは⑤か⑥に絞られたね。
物理が苦手な文子
とりあえず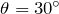，\theta=30^\circとして，今計算した条件式を表しておこうか。

    \begin{eqnarray*}v^2\sin^2 30^\circ&<&2gh\\v^2&<&8gh\end{eqnarray*}

物理が得意な秀樹
あとは落下点までの距離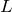Lを求めよう。
物理が苦手な文子
水平方向は等速で，時間はさっき求めたtだから，

    \begin{eqnarray*}L&=&v\cos\theta\cdot\frac{2v\sin\theta}{g}\\&=&v\cos30^\circ\cdot\frac{2v\sin30^\circ}{g}\\&=&v\cdot\frac{\sqrt3}{2}\cdot\frac{v}{g}\\&=&\frac{\sqrt3 v^2}{2g}\end{eqnarray*}

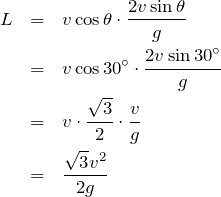
物理が得意な秀樹
ここで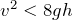，v^2<8ghを考慮してみよう。
物理が苦手な文子
こういうこと？

    \begin{eqnarray*}L&=&\frac{\sqrt3 v^2}{2g}<\frac{\sqrt3}{2g}\cdot 8gh\\L&<&4\sqrt3 h\end{eqnarray*}

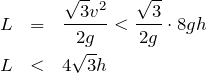
物理が得意な秀樹
そういうことだね。答えは⑤だ。
タイトルとURLをコピーしました