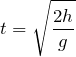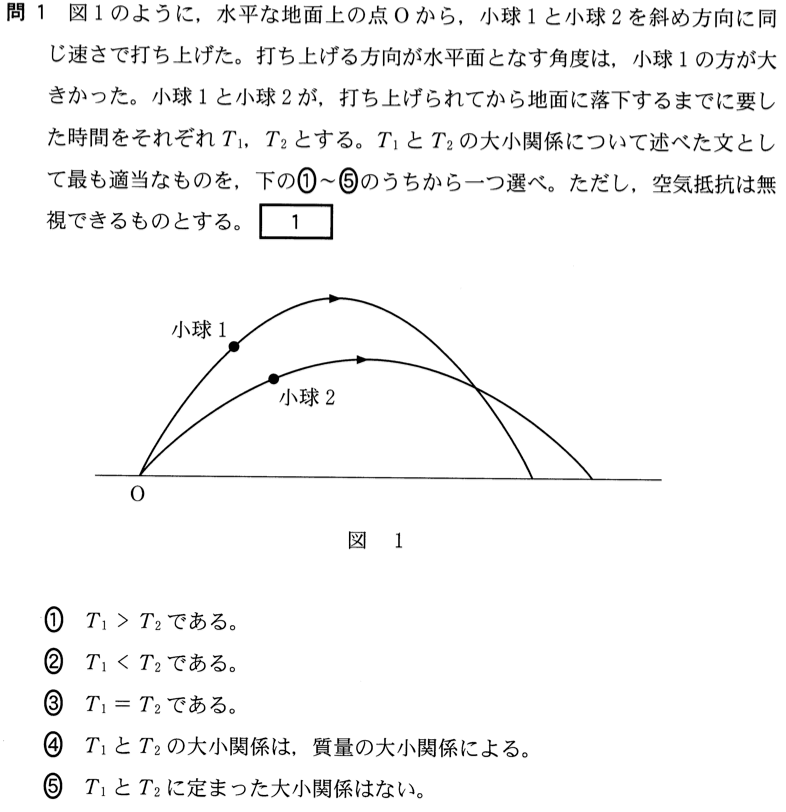
打ち上げの速さが同じなんだから、角度が違っても、落ちてくるまでの時間は同じよね?
だって図を見ても、2つの小球が飛んでいく曲線もだいたい同じ長さじゃない?
そう言われれば、同じくらいの長さだね。じゃあ、例えば真上に投げるとして、高くまで上がった場合と、低くしか上がらなかった場合では、どちらの飛行時間が長い?
それは高い方でしょ。でもそれは、高くまで上がる方が初速度が大きいからでしょ。この問題は角度は違うけど、打ち上げる速さは同じじゃない。
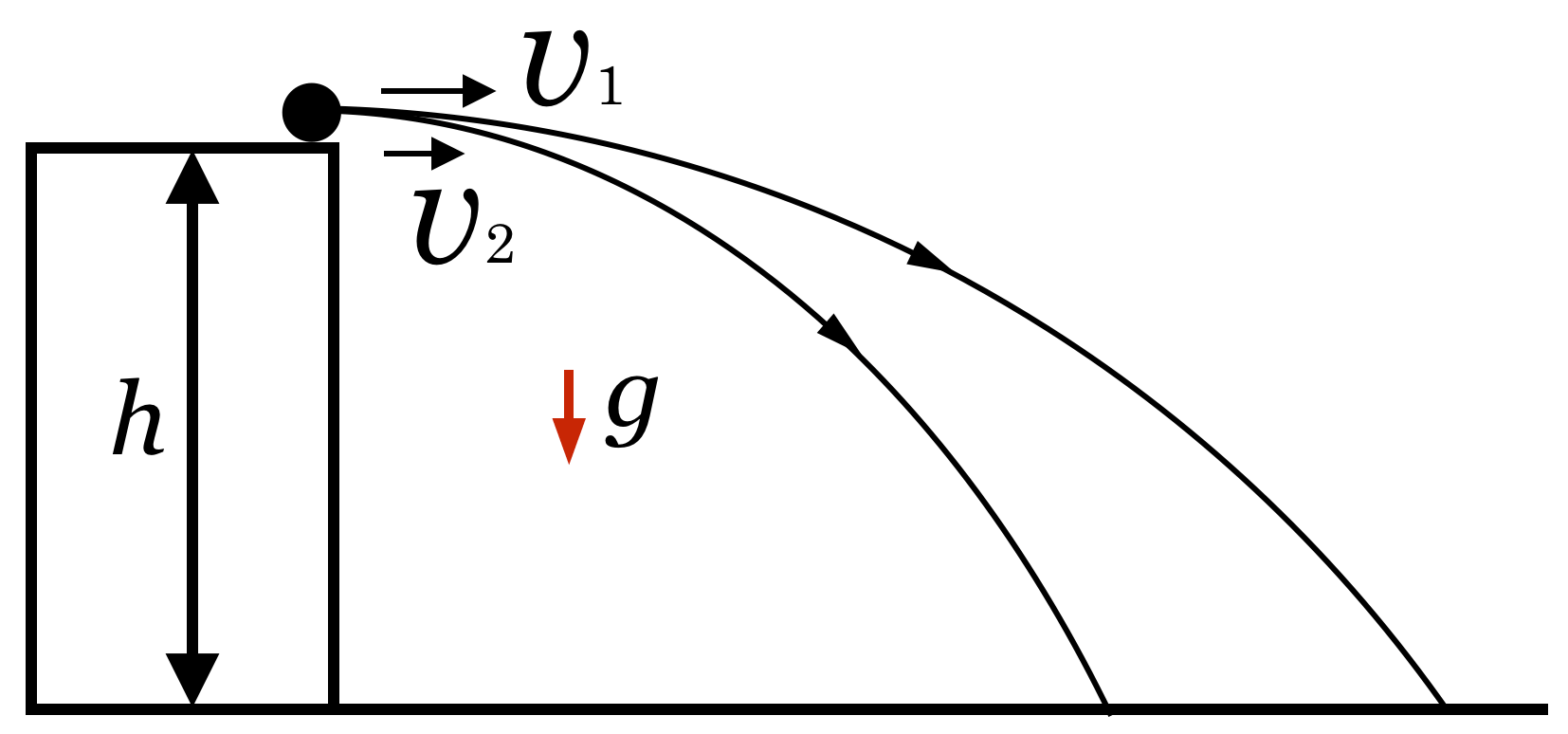
まぁそうだね。でもこの問題の図では小球1の方が高くまで上がってるから、小球1の方が飛行時間が長い可能性は無いかな?
確かに小球1の方が高くまで上がってるけど、小球2の方が遠くまで飛んでるから、飛行時間は同じくらいになると思うんだけど?
じゃあ、同じ高さからの水平投射で考えてみようか。初速度を変えて同じ高さから水平に投げ出してみると、どっちの方が早く地面に着くかな?
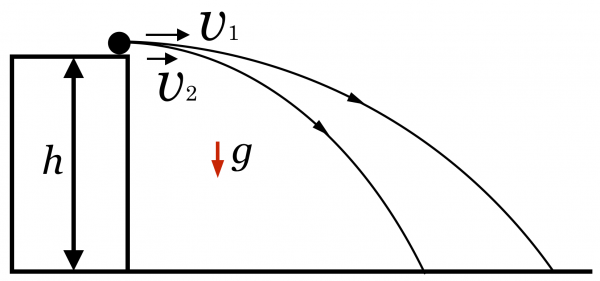
見たことあるわ。確かこれって地面に着く時間は同じなんじゃなかったっけ。鉛直方向の運動だけ考えると、自由落下と同じなのよね。地面に着くまでの時間

は、鉛直下向きを正として考えると、
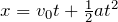
より、
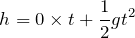
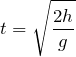
そうだよね。ということは、最初の問題に戻るとどうなるかな?
落下までの時間は、鉛直方向の運動だけ考えればいいのか。ということは、高く上がった小球1の方が時間が長いので、答えは①になるということね。水平方向の距離は関係ないというのは、なんとなく納得できないけど。
水平投射の時も水平方向の距離は関係ないんだから、同じだね。ということで、答えは①だ。


![]() は、鉛直下向きを正として考えると、
は、鉛直下向きを正として考えると、![]() より、
より、![]()
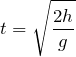
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!

![]() は、鉛直下向きを正として考えると、
は、鉛直下向きを正として考えると、![]() より、
より、![]()