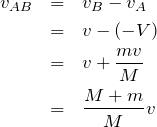
相対速度を求める問題だね。相対速度って何なのか分かっているかな?
動いている観測者から見た物体の速度よね。Aに対するBの相対速度
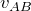
は、
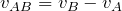
となるんだよね。
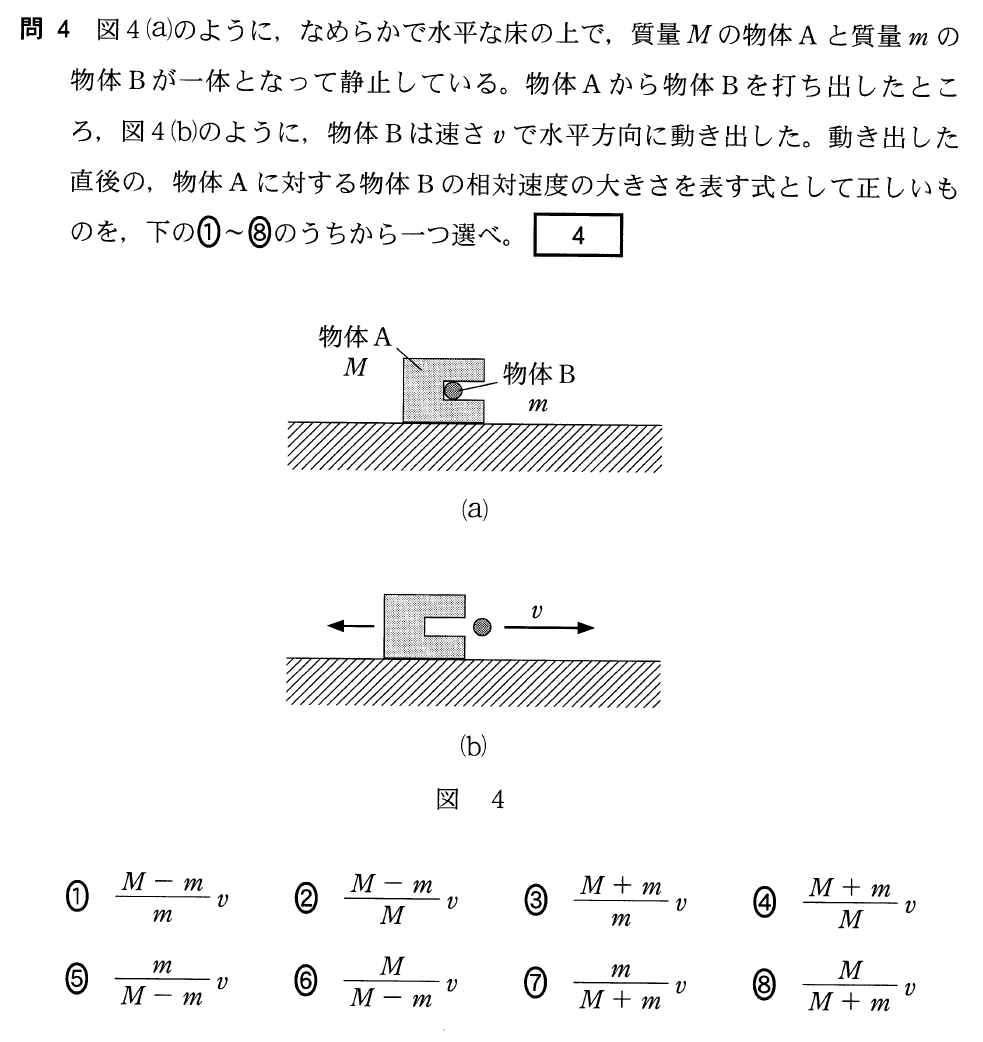
その通り。ということは打ち出した後の物体Aの速度が分かればいいね。この問題では、1つにくっついていた物体が、2つに分裂しているね。このような場合、まず何を考えるか分かるかな?
確か、2つの物体が衝突したり、2つの物体が1つに合体したり、1つの物体が2つに分裂したりするときは、「運動量保存の法則」を使うんだったと思うけど。
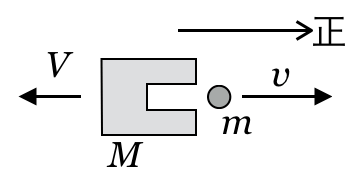
そうだね。じゃあまず「運動量保存の法則」を使って式を立ててみようか。図のように、衝突後の物体Aの速さを

とするとどうなるかな?
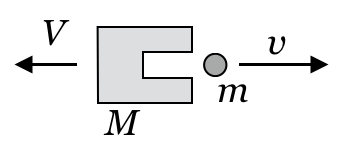
ちょっと待って。

でいいの?
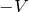
じゃないの?
なるほど。確かに問題に左向きの矢印が描いてあるし、どう考えても左に動くよね。そういう意味では
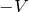
と書いてもいいんだ。ちゃんと理解していればどっちでもいいんだけど、おすすめは

かな。あくまでも図に書くのは”大きさ”で、”向き”は矢印の向きで表すんだ。そして式を立てるときに

にするか、
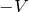
にするかを矢印の向きに合わせて書けばいいんだな。
この問題のように一直線上の動きなら問題ないけど、平面の動きだともう正負で向きを表せないからね。だからあくまでも図に書くのは”大きさ”と決めておいた方がいいと思うよ。
なるほどね。じゃあ、「運動量保存の法則」の式は・・・
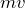
よね。
そうだね。あともう一つ大事なことがあって、運動量はベクトルなので向きをちゃんと考えてね。
さっきから向きの話しをしてるから、さすがに注意するわ。
ちなみにエネルギーには向きが無いから、力学的エネルギー保存の法則で式を立てるときには向きは考えなくていいんだよ。
右向きを正として、「分裂前の運動量の和」=「分裂後の運動量の和」で式を立ててみよう!
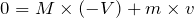
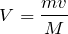
いいね。じゃあ、相対速度を求めよう。こっちも向きに注意してね。
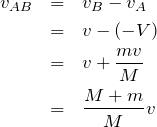

![]() は、
は、![]() となるんだよね。
となるんだよね。![]() とするとどうなるかな?
とするとどうなるかな?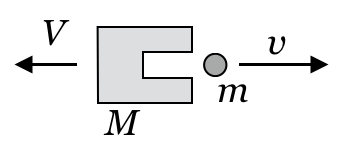
![]() でいいの?
でいいの?![]() じゃないの?
じゃないの?![]() と書いてもいいんだ。ちゃんと理解していればどっちでもいいんだけど、おすすめは
と書いてもいいんだ。ちゃんと理解していればどっちでもいいんだけど、おすすめは![]() かな。あくまでも図に書くのは”大きさ”で、”向き”は矢印の向きで表すんだ。そして式を立てるときに
かな。あくまでも図に書くのは”大きさ”で、”向き”は矢印の向きで表すんだ。そして式を立てるときに![]() にするか、
にするか、![]() にするかを矢印の向きに合わせて書けばいいんだな。
にするかを矢印の向きに合わせて書けばいいんだな。![]() よね。
よね。
![]()
![]()
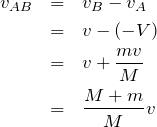
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!
![]() は、
は、![]() となるんだよね。
となるんだよね。![]() とするとどうなるかな?
とするとどうなるかな?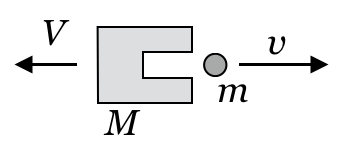
![]() でいいの?
でいいの?![]() じゃないの?
じゃないの?![]() と書いてもいいんだ。ちゃんと理解していればどっちでもいいんだけど、おすすめは
と書いてもいいんだ。ちゃんと理解していればどっちでもいいんだけど、おすすめは![]() かな。あくまでも図に書くのは”大きさ”で、”向き”は矢印の向きで表すんだ。そして式を立てるときに
かな。あくまでも図に書くのは”大きさ”で、”向き”は矢印の向きで表すんだ。そして式を立てるときに![]() にするか、
にするか、![]() にするかを矢印の向きに合わせて書けばいいんだな。
にするかを矢印の向きに合わせて書けばいいんだな。![]() よね。
よね。
![]()
![]()