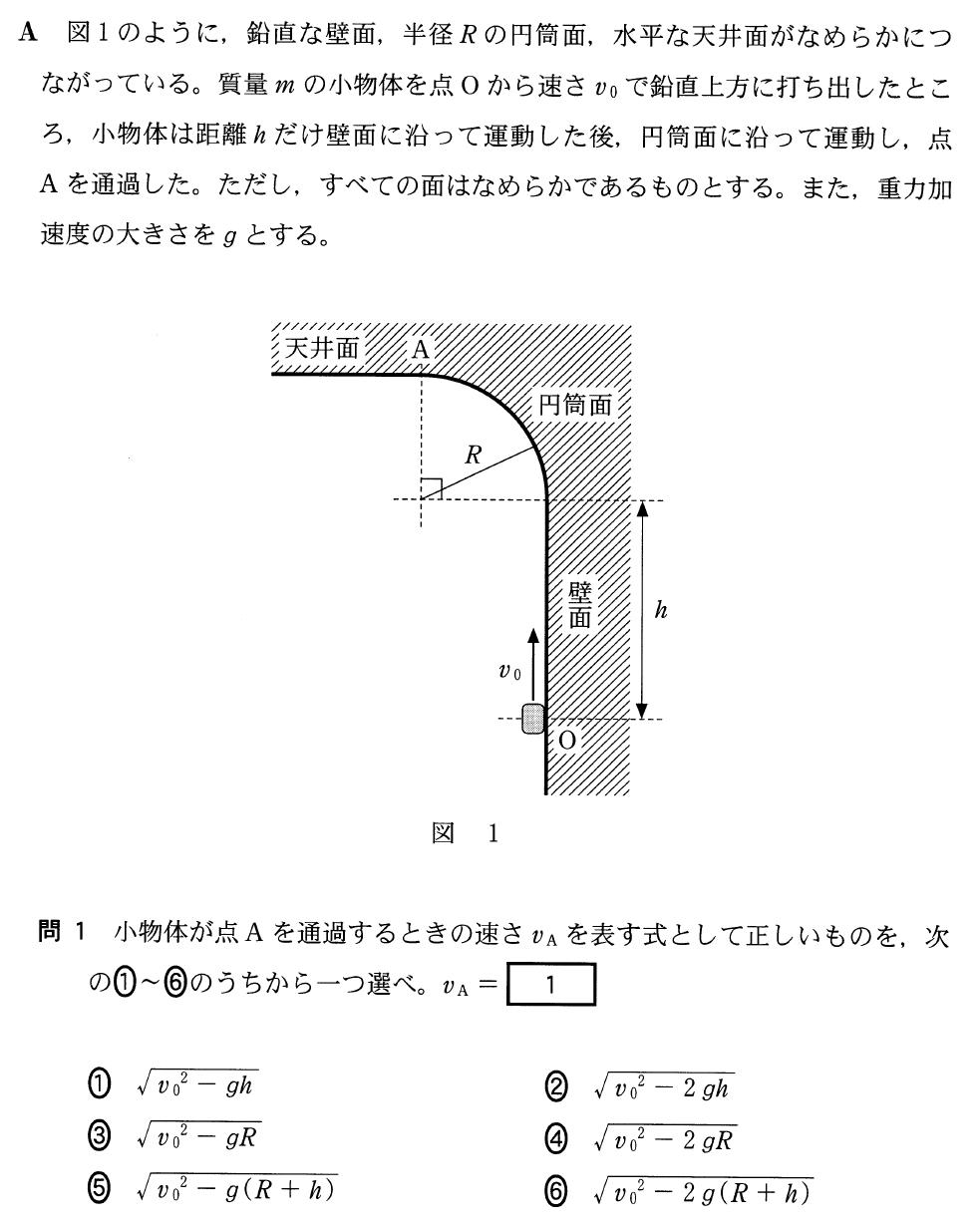
あんまり見かけない図だけど、問題を読む限り力学的エネルギー保存の法則で計算ができそうな気がするわ。
鋭いね。壁に沿って鉛直上方に上がっていくっていう問題は僕も見たことないけど、考え方は難しくないね。力学的エネルギー保存の法則を使うときに大切なのは、どの点とどの点で力学的エネルギーが保存されているのかを、しっかりと確認することだね。
「点Oでの力学的エネルギー」=「点Aでの力学的エネルギー」という式を立てれば良いんだ。ところで確認だけど、力学的エネルギーって何?
えっと、確か、「運動エネルギーと位置エネルギーの和」ね。
そうだね。そもそも「和」なんだよね。それと、高校では位置エネルギーが何種類か出てくるね。
そうだね。じゃあ、力学的エネルギー保存の法則の式を立ててみようか。そうそう、重力による位置エネルギーの基準を決めてからだね。
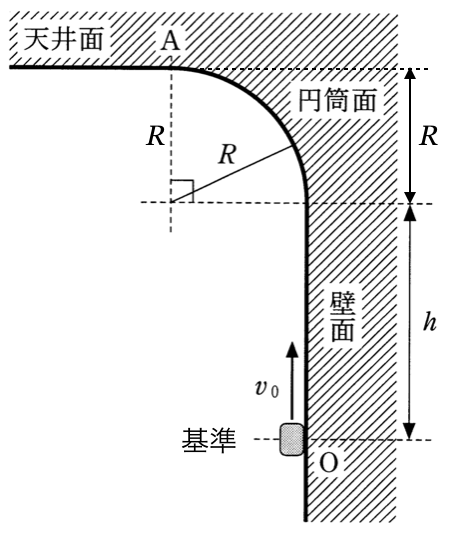
重力による位置エネルギーの基準は点Oでいいわよね。そうすると、点Aの高さは
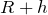
になるので、
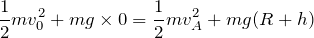
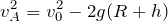
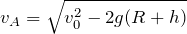
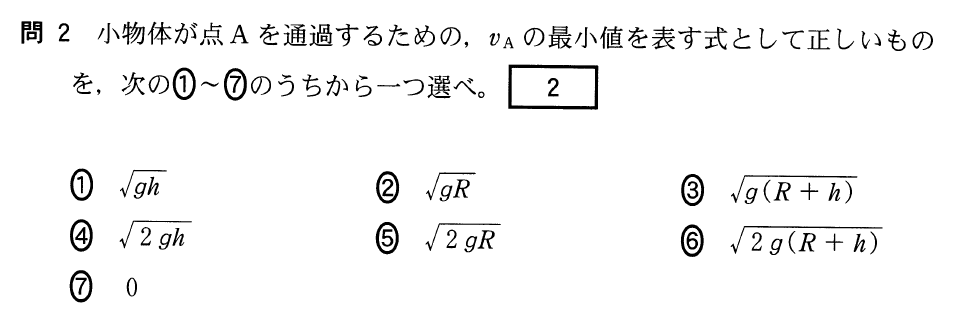
そうだね。良くある問いなんだけど、式で考えるのは苦手な人が多いね。点Aを通過するっていうのは、途中で壁から離れずに、点Aでも天井に接触しているっていうことだよね。
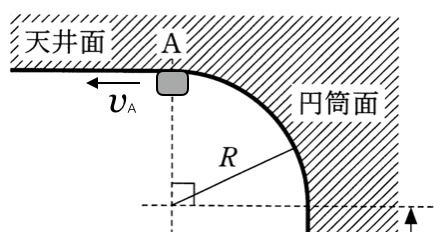
そこまでは分かるわ。でもその「接触している」っていう条件をどうやって式にするの?
簡単だよ。天井から受ける垂直抗力が0以上であれば良いんだ。つまり、接触していれば垂直抗力が存在するっていうことだね。一般的に力の矢印を描くときも、接触しているから垂直抗力を描くでしょ。
なるほどね。点Aでの垂直抗力≧0だと点Aを通過するっていうことになるのね。ということは、まず点Aでの力の矢印を描かなきゃダメね。
まず重力と、天井からの垂直抗力、この垂直抗力は天井から受けるんだから、下向きで良いのよね。
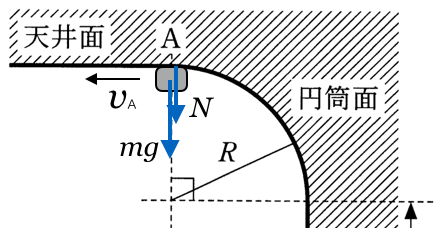
そうだよ。なんか変な感じがするかもしれないけど、間違いなく鉛直下向きだ。
そんな感じがするかもしれないけど、力の向きと運動の向きは直接は関係ないんだよ。だらか力が下向きで、運動の方向が左向きでも何の問題もないんだね。力と関係があるのは加速度の向きだよ。運動方程式
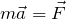
はそのことを表しているね。というわけで、力の矢印を描いたら、運動方程式だ。まずは加速度の向きはどっちかな?
今の話の流れだと、加速度の向きと力の向きには関係があるので、加速度も下向きでしょ。
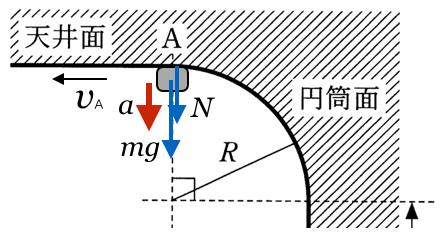
そうだね。そもそも、点Aまでは円運動をしているので、円の中心方向が加速度の向きなんだ。つまり、下向きだね。
そうとも考えられるのか。なるほどね。じゃあ、下向きを正として運動方程式を立てるよ。
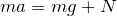
円運動なので、
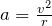
を使って、
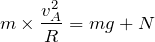
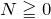
であればよいので、
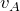
が最小となるのは
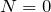
のとき。つまり、
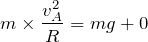
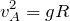
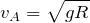


![]() になるので、
になるので、 ![]()
![]()
![]()



![]() はそのことを表しているね。というわけで、力の矢印を描いたら、運動方程式だ。まずは加速度の向きはどっちかな?
はそのことを表しているね。というわけで、力の矢印を描いたら、運動方程式だ。まずは加速度の向きはどっちかな?
![]()
![]() を使って、
を使って、 ![]()
![]() であればよいので、
であればよいので、![]() が最小となるのは
が最小となるのは![]() のとき。つまり、
のとき。つまり、 ![]()
![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!

![]() になるので、
になるので、 ![]()
![]()
![]()



![]() はそのことを表しているね。というわけで、力の矢印を描いたら、運動方程式だ。まずは加速度の向きはどっちかな?
はそのことを表しているね。というわけで、力の矢印を描いたら、運動方程式だ。まずは加速度の向きはどっちかな?
![]()
![]() を使って、
を使って、 ![]()
![]() であればよいので、
であればよいので、![]() が最小となるのは
が最小となるのは![]() のとき。つまり、
のとき。つまり、 ![]()
![]()
![]()