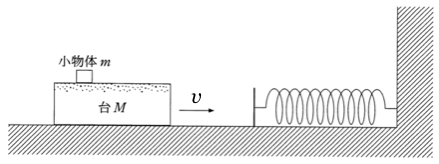
力学的エネルギー保存の法則で、解けそうな感じがするけど・・・
そうだね。やってみよう。どの点とどの点で力学的エネルギー保存の法則を立てるのかを確認してから立てようか。
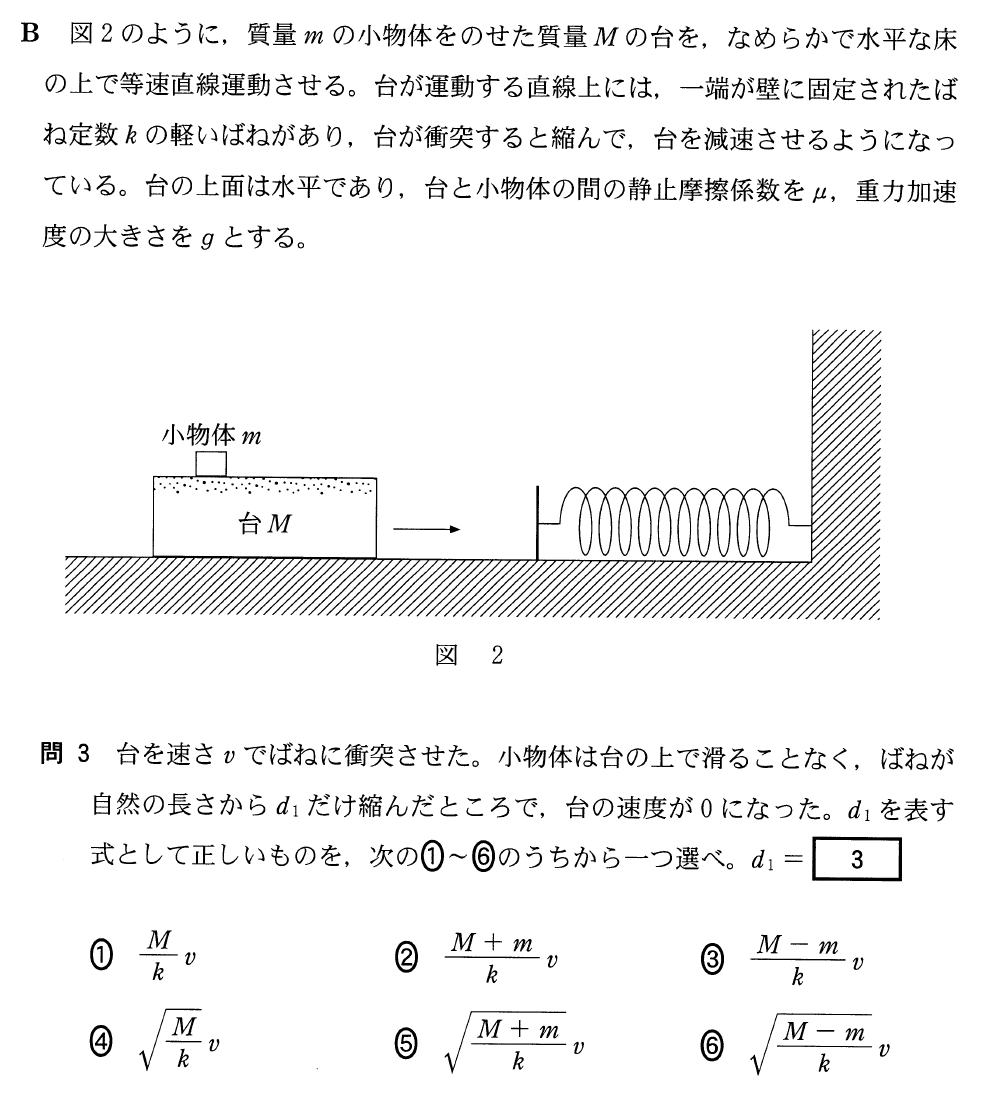
ばねに衝突する前と、ばねが
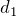
だけ縮んで台の速度が0になった点で立てればいいわね。
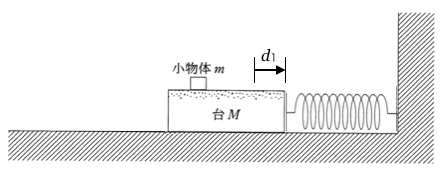
この場合の力学的エネルギーは「運動エネルギー+弾性力による位置エネルギー」でいいわね。
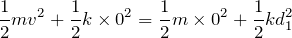
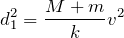
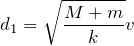
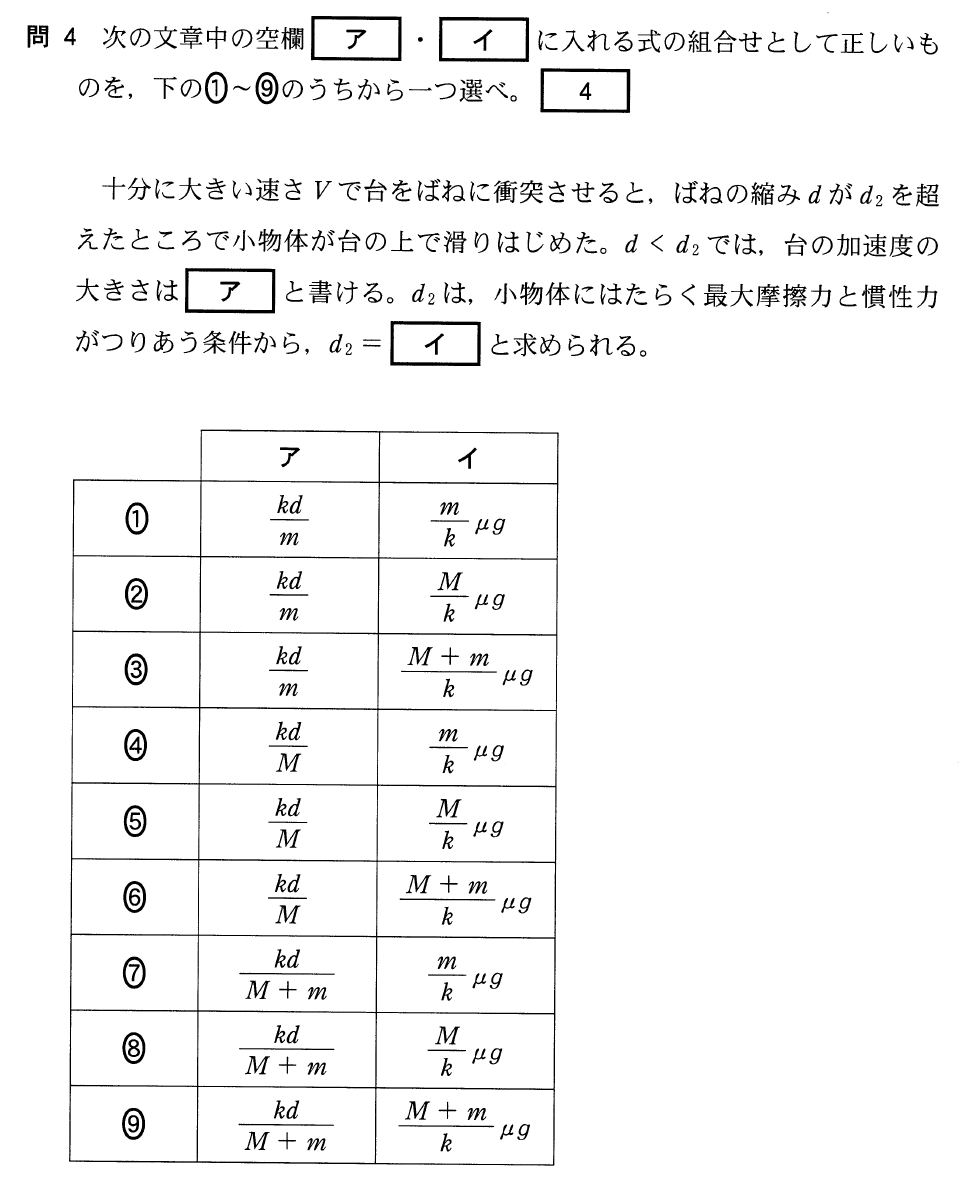
だいたいイメージできていると思うわ。最初は
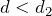
だから、台の上の小物体はまだ滑ってないのよね。
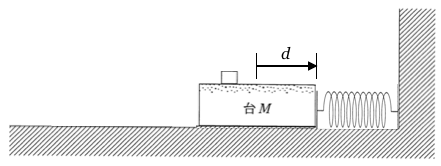
ということは、台と小物体を1つの物体として考えて良いのよね。
その通りなんだけど、イの空欄が台と小物体を別々に考えないとダメな問題なので、練習としてこの問題でも別々に考えてみない?
そうなの?別々に考えるっていうことは、別々に力の矢印を描くっていうこと?
そうだよ。一体として考えた方が簡単だけど、練習!練習!
じゃあ、まずは小物体にはたらく力の矢印を描こうかな。重力があって、台と接しているから垂直抗力があって、さらに摩擦力があるのよね。あれ?摩擦力の向きってどっち?
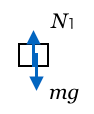
摩擦力の向きの求め方って、いろいろあるけど、とりあえずは摩擦がない時を考えてみようか。台はばねに押されて減速することを考えると、小物体は摩擦がなければ台の上をどっちに滑るかな?
摩擦がなければ小物体には水平方向の力がはたらいていないから、慣性の法則に従って減速せずに動くわね。つまり、台の上を右に滑るかな?
そうだね。摩擦がなければ右に滑る、でも今は摩擦があるから右に滑らない、ということは摩擦の向きどっち?
そうか、左向きね。右に滑るはずなのにそれを摩擦が妨げているということね。
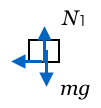
摩擦力の式って
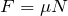
じゃなかったっけ。
その式が使えるのは、最大摩擦力か、動摩擦力だね。小物体は台に対しては静止しているので、この場合は静止摩擦力を考えるんだ。
直接静止摩擦力を求める式っていうのはないので、力のつり合いの式を立てて求めたりするんだね。ただ、この問題では静止摩擦力の大きさは必要がないので、そのまま
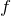
として、次に進もう。
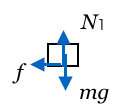
ちょっと待って!問題文に「静止摩擦係数を
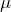
って書いてあるわよ。
そうだね。ここもややこしいところなんだけど、「動摩擦係数」は「動摩擦力」の式に出てくるけど、「静止摩擦係数」は「最大摩擦力」の式に出てくるんだ。だから「静止摩擦係数」と「静止摩擦力」は関係がないんだ。
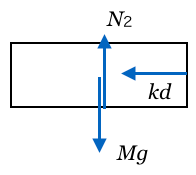
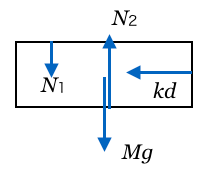
そとりあえずこまではいいかな。次は台にはたらく力の矢印を描こう。重力と床からの垂直抗力とばねの弾性力は良いよね。ちなみにばねの縮みは
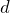
だからね。あと、小物体と接しているから、小物体からも力を受けるんだけど、どんな力を受けるか分かるかな?
小物体の質量が
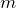
だから、
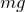
じゃないの?
この問題では
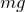
で良いんだけど、一般的にはその考えだとダメなこともあるんだ。さらに、
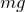
以外の力もあるしね。
「作用反作用の法則」を考えて欲しいんだ。例えば、さっきの小物体にはたらく垂直抗力って、「台が小物体を押す力」でしょ。この力に対してかならず反作用が存在して、それは「小物体が台を押す力」なんだよ。
「小物体が台を押す力」ということは、これは台にはたらく力ね。
そうなんだよ。台は小物体から
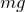
という力を受けていると考えるんじゃなくて、小物体にはたらく垂直抗力の反作用を受けていると考えるんだ。
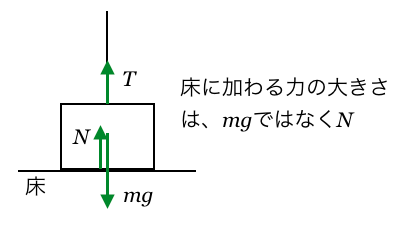
この問題では同じなんだけど、例えば小物体を上から糸で少しだけ引っ張っている状態の時、台にはたらく力は
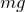
じゃなくて、垂直抗力の反作用と考えないと正しい値にならないんだよ。
ということは、小物体が受けている摩擦力と、同じ大きさで逆向きの摩擦力が台にはたくということね。
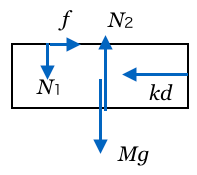
力の矢印はこれで完成だ。今求めたいのは台の加速度の大きさなんだけど、加速度はどっち向きかな?
台は右向きに運動しているけど減速しているんだから、加速度は左向きかな。
そうだね。小物体も同じ加速度なので、図の中に描いておこう。ここまで準備したら、次は何をしようかな?
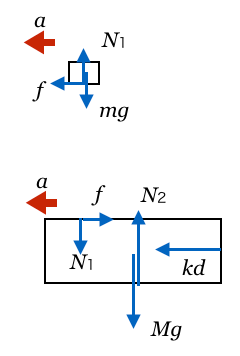
力の矢印と加速度を描いたら、正の向きを決めて運動方程式を立てるのね。加速度に合わせて左向きを正とすると、最初に小物体の運動方程式。
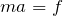
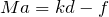
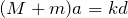
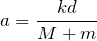
ここまでは合ってるぞ。かなり苦労したけど、最初に言ったとおり、台と小物体を一体として考えたら簡単なんだよね。
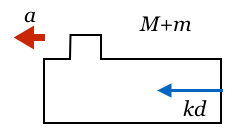
鉛直方向の力の矢印はこの運動と関係ないので省略すると、このような図になって、
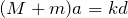
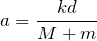
まぁいいじゃない。苦労した分、理解が深くなっているよ。
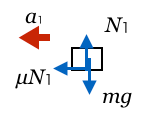
それじゃあ、後半は小物体だけ考えるよ。ばねの縮みが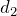 のとき、小物体にはたらく力の矢印はどう描けるかな?
のとき、小物体にはたらく力の矢印はどう描けるかな?
接触しているものが台しかないから、さっきと同じよね。
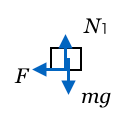
そうだね。だけど、ばねの縮みが
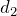
を超えると小物体は滑り始めるので、その瞬間ということは最大摩擦力が使えるね。ついでに、加速度も描いちゃおうか。さっきと違うので
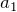
としておこう。
ちなみに
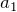
って、どうなるかな。
ばねの縮みが
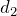
のときの加速度だから、さっきの答えを使うと、
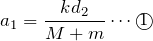
そうだね。さて、最後に問題文にある「慣性力」って何か分かるかな。
聞いたことはあるんだけど・・・。確か慣性の法則とはあまり関係がないのよね。
慣性の法則と関係ないっていうわけではないけど、気にする必要はないね。観測者が加速しているとき、物体には加速度と逆向きに
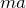
の大きさの力がはたらいているように見えて、この力を「慣性力」っていうんだ。
聞いたことはある。だけどどうやって使うのかは分からないわ。
小物体と同じ加速度で運動している人を観測者とするんだ。小物体の上に人が乗っているイメージね。そうすると、観測者にとっては小物体は静止して見えるでしょ。ということは、力がつりあって見えているということなんだ。
慣性力を図の中に描いてみると、加速度の向きは左なので、慣性力は右向きで大きさは
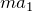
なんだ。
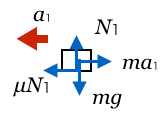
なるほど。それで問題文に最大摩擦力と慣性力がつりあうって書いてあるのか。
水平方向の力はこの2つしかないからね。それじゃあ、力のつりあいの式を書いてみて。
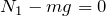
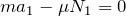
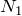
を消去して、
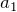
に①を代入すると、
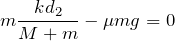
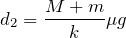

![]() だけ縮んで台の速度が0になった点で立てればいいわね。
だけ縮んで台の速度が0になった点で立てればいいわね。

![]()
![]()
![]()

![]() だから、台の上の小物体はまだ滑ってないのよね。
だから、台の上の小物体はまだ滑ってないのよね。
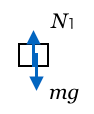

![]() じゃなかったっけ。
じゃなかったっけ。![]() として、次に進もう。
として、次に進もう。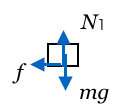
![]() って書いてあるわよ。
って書いてあるわよ。![]() だからね。あと、小物体と接しているから、小物体からも力を受けるんだけど、どんな力を受けるか分かるかな?
だからね。あと、小物体と接しているから、小物体からも力を受けるんだけど、どんな力を受けるか分かるかな?
![]() だから、
だから、![]() じゃないの?
じゃないの?![]() で良いんだけど、一般的にはその考えだとダメなこともあるんだ。さらに、
で良いんだけど、一般的にはその考えだとダメなこともあるんだ。さらに、![]() 以外の力もあるしね。
以外の力もあるしね。![]() という力を受けていると考えるんじゃなくて、小物体にはたらく垂直抗力の反作用を受けていると考えるんだ。
という力を受けていると考えるんじゃなくて、小物体にはたらく垂直抗力の反作用を受けていると考えるんだ。
![]() じゃなくて、垂直抗力の反作用と考えないと正しい値にならないんだよ。
じゃなくて、垂直抗力の反作用と考えないと正しい値にならないんだよ。


![]()
![]()
![]()
![]()

![]()
![]()
![]() のとき、小物体にはたらく力の矢印はどう描けるかな?
のとき、小物体にはたらく力の矢印はどう描けるかな?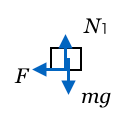
![]() を超えると小物体は滑り始めるので、その瞬間ということは最大摩擦力が使えるね。ついでに、加速度も描いちゃおうか。さっきと違うので
を超えると小物体は滑り始めるので、その瞬間ということは最大摩擦力が使えるね。ついでに、加速度も描いちゃおうか。さっきと違うので![]() としておこう。
としておこう。
![]() って、どうなるかな。
って、どうなるかな。![]() のときの加速度だから、さっきの答えを使うと、
のときの加速度だから、さっきの答えを使うと、![]()
![]() の大きさの力がはたらいているように見えて、この力を「慣性力」っていうんだ。
の大きさの力がはたらいているように見えて、この力を「慣性力」っていうんだ。![]() なんだ。
なんだ。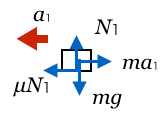
![]()
![]()
![]() を消去して、
を消去して、![]() に①を代入すると、
に①を代入すると、![]()
![]()