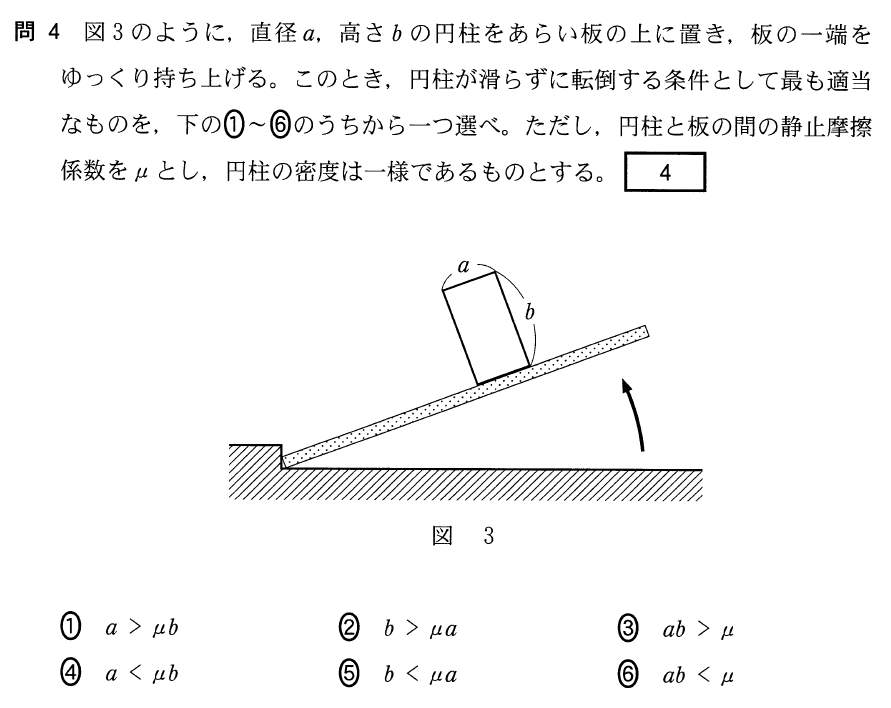
斜面上を滑る問題はよく見るけど、転倒するのはやったことないわ。
そうだね。でも時々ある問題なんだよね。しかも知っているのと知らないのとでは、難しさが大きく変わるので、一度やったら覚えておいた方が良いよ。
まず「滑らずに転倒する条件」だから、「滑らない」条件を先に考えようか。
それならやったことあるわよ。この場合だと、重力の斜面下方成分より最大摩擦力が大きければ良さそうよね。
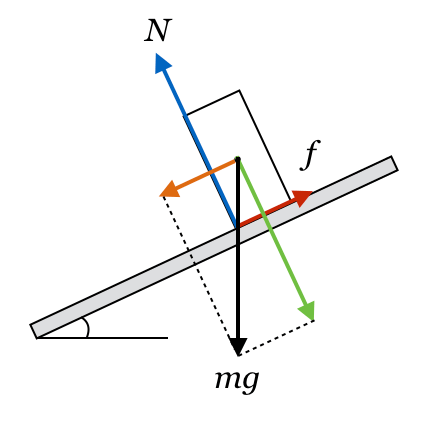
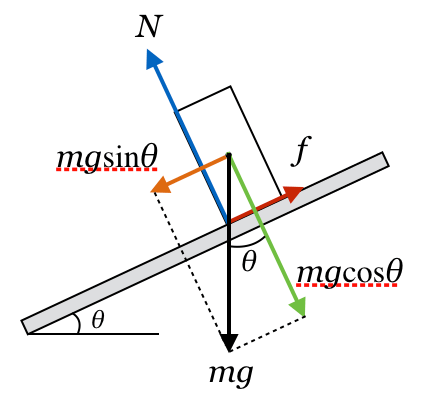
そうだね。あとは転倒する条件だね。実は図を描くとすぐ分かるんだよ。
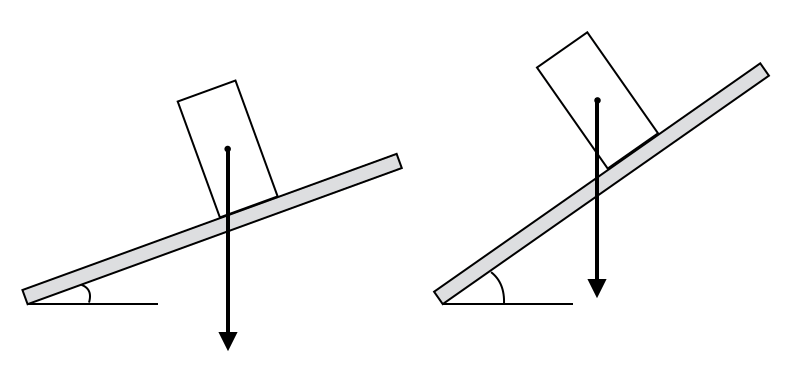
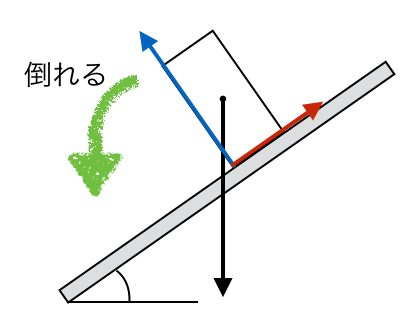
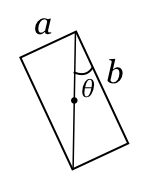
ちなみにこの図だと、左は倒れないけど、右は倒れるんだ。
重力の矢印がどこを通っているのかで、分かるんだ。重力の矢印が、底面と交わっていれば倒れないけど、交わっていなければ倒れるんだ。
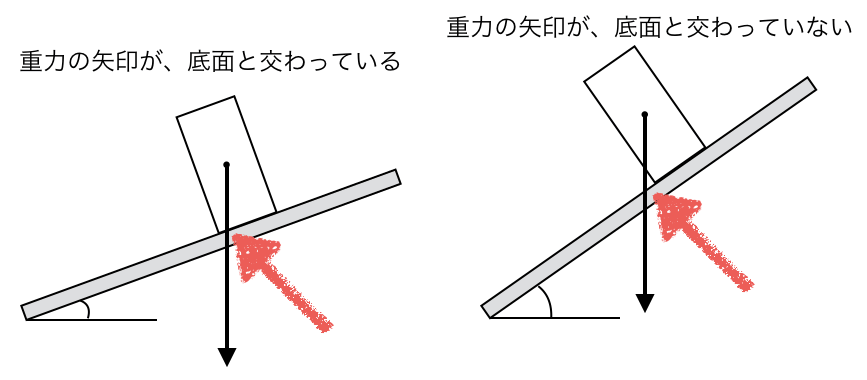
そういうことなの?難しくはないし、理解しやすいわ。
でしょ。なぜこうなるかというと、力のモーメントがつりあっていれば倒れないけど、つりあっていなければ倒れるということなんだ。
モーメント?まぁそうか。倒れるっていうことは、回転するっていうことか。
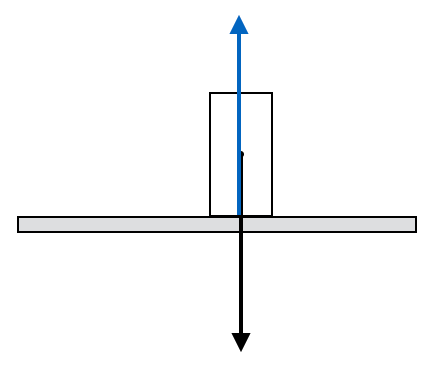
まずは傾いていないときの図から考えようか。板が傾いていなければ、重力と垂直抗力だけで、摩擦力はないよね?
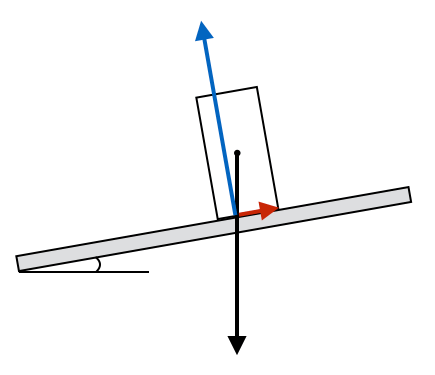
板を徐々に傾けていくと、静止摩擦力が徐々に大きくなっていくよね。実はその時に、垂直抗力の作用点が斜面下方に移動していくんだよ。
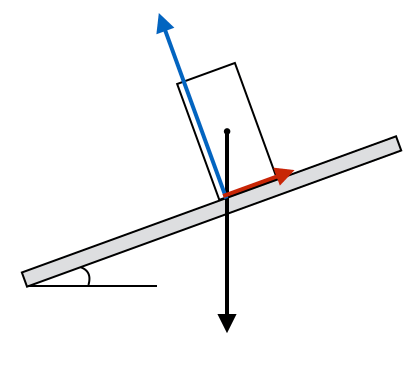
えっ?どういうこと?垂直抗力って底面の真ん中に描くんじゃないの?
斜面だったり、水平でも横方向の力がはたらいているときには、垂直抗力は真ん中ではないんだ。これは、垂直抗力の作用点が底面の真ん中だと絶対に力のモーメントがつりあわないんだ。物体は回転していないので、力のモーメントはつりあっているはずで、ということは、垂直抗力の作用点は真ん中ではないんだね。で、どこになるかというと、この場合は重力の矢印と底面の交点が作用点なんだ。
板の角度を大きくしていって、重力の矢印が角に来るときまでは物体は倒れない。垂直抗力の作用点が角にあると考えられるからね。ところが重力の矢印と、底面の交点が無くなると倒れるんだよ。垂直抗力は角までしか移動できないから、力のモーメントがつりあわなくなるんだね。

まとめると、倒れるぎりぎりの角度は、重力の矢印が物体の角に来たときね。その時に滑らない条件を満たしていれば、ぎりぎり倒れない。その角度をちょとでも超えると転倒するのね。
じゃあ、そのぎりぎりの角度を
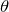
として計算してみようか。
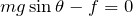
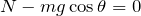
ここで、滑らないためには、静止摩擦力
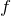
が最大摩擦力
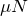
より小さければいいので、

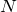
を消去すると、
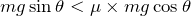
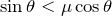
今、
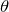
は与えられていなかったので、
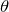
を求める必要があるね。
重力の線をまっすぐ上に延ばしてみると、ちょうど図の長方形の対角線になるよね。対角線の長さは三平方の定理で求まるから、
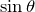
、
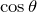
が求まるね。
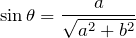
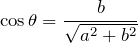
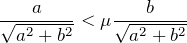
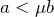









![]() として計算してみようか。
として計算してみようか。
![]()
![]()
![]()
![]()
![]()
![]() は与えられていなかったので、
は与えられていなかったので、![]() を求める必要があるね。
を求める必要があるね。![]() 、
、![]() が求まるね。
が求まるね。
![]()
![]()
![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!








![]() として計算してみようか。
として計算してみようか。
![]()
![]()
![]()
![]()
![]()
![]() は与えられていなかったので、
は与えられていなかったので、![]() を求める必要があるね。
を求める必要があるね。![]() 、
、![]() が求まるね。
が求まるね。
![]()
![]()
![]()
![]()
コメント
[…] 2016年度追試第1問 問4「斜面上の物体が転倒する条件」 […]