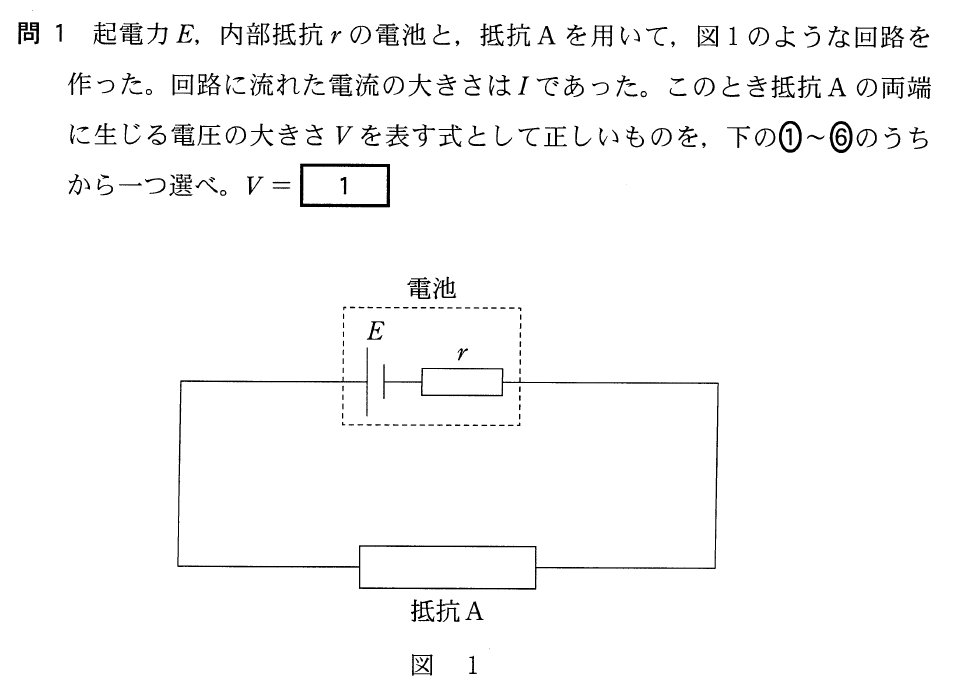
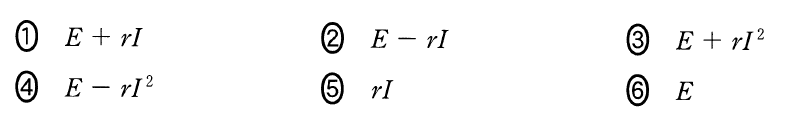
電気回路の問題ね。シンプルな回路だけど、内部抵抗があるのは、少し嫌な感じだわ。
内部抵抗といっても、単に電気抵抗と考えていいから大丈夫だよ。式を立ててみようか。
内部抵抗を単に電気抵抗と考えてよいのであれば、内部抵抗と抵抗Aの直列回路っていうこと?
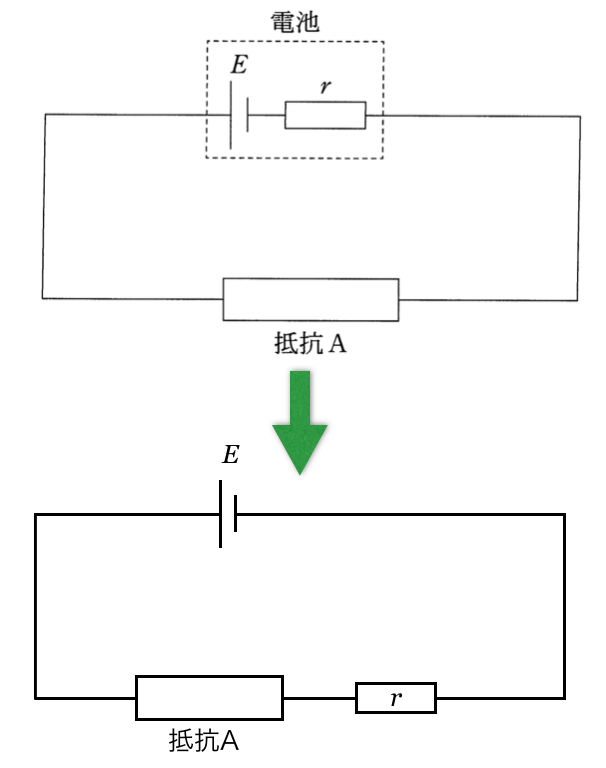
抵抗が直列の場合、合成抵抗は単純に足すだけだけど、この問題では抵抗Aの値が出ていないのよね。
そうだね。合成抵抗は求まらないね。でも抵抗Aの電気抵抗を
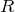
とおいてみたら?
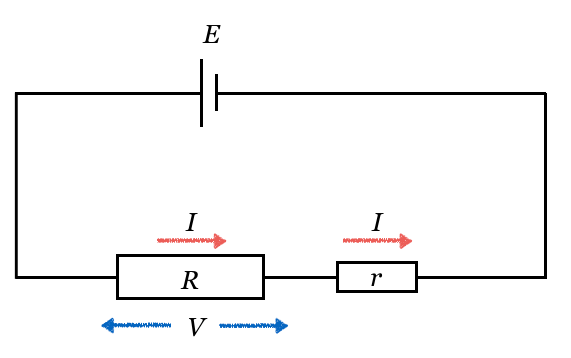
ということは、

と
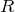
の合成抵抗なので、直列だから
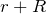
ね。流れる電流は
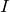
だから、オームの法則より、
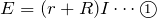
そもそも、
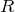
は与えられていないのと、まだ抵抗Aの両端の電圧

を使ってないね。
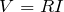
となるから、①と合わせて
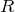
を消去すると、
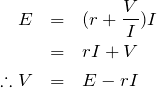
そうだね。答えは②だ。答えは出たんだけど、電位の考え方ができると様々な応用が利くので、この問題でちょっとだけ説明させて。
ルールは簡単なんだ。
・つながっている金属は等電位
・電流が抵抗を流れると
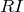
だけ電位が下がる
・電池は負極から正極へ電位を

だけ上げる
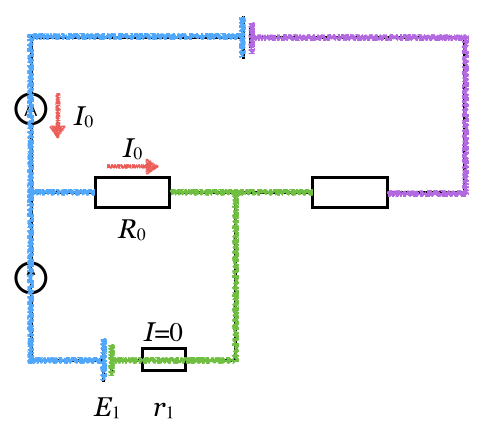
この考え方を問題の回路に当てはめると、この図になるよ。
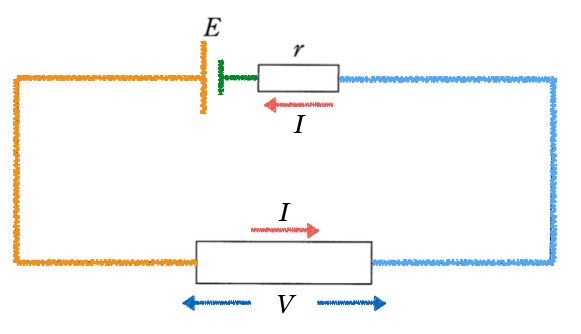
そういうことだ。あとはある点から出発して、回路のどこかを回って、元の点に戻ったら、電位も元に戻る、という式を立てるんだ。
どこかを回って戻る、ということは、キルヒホッフの第2法則みたいなもの?
その通り!キルヒホッフの第2法則、そのままだね。それじゃあ、電池の負極から左回りで電位を追っていこう。
まず電池で電位が
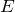
だけ上がって、抵抗Aで電位が
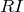
だけ下がって、
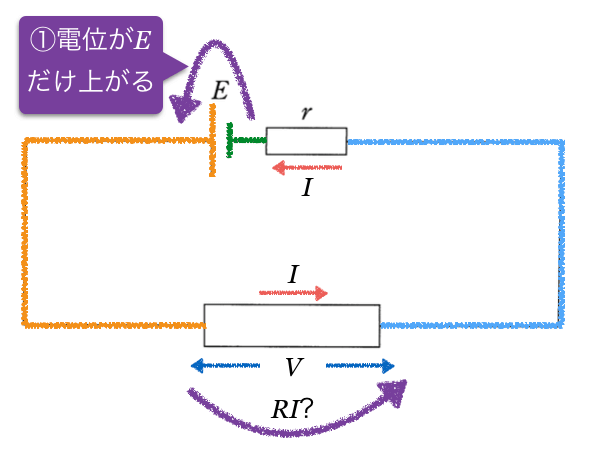
ちょっと待って。確かに
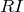
だけ下がるんだけど、もともと抵抗Aの電圧は

と与えられているから、ここは

だけ電位が下がる、ということなんだよ。
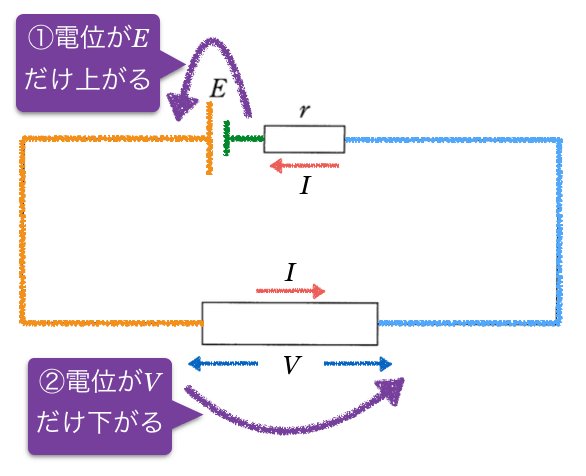
電圧が

というだけでは、どっちの電位が高いのか分からないけど、電流の向きが分かっているじゃない。電流って、必ず電位の高い方から低い方へ流れるんだよ。つまり電流の流れる方へ電位が下がるんだ。
そういうことね。さらに進んで、内部抵抗を考えると電位が
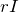
下がるのね。
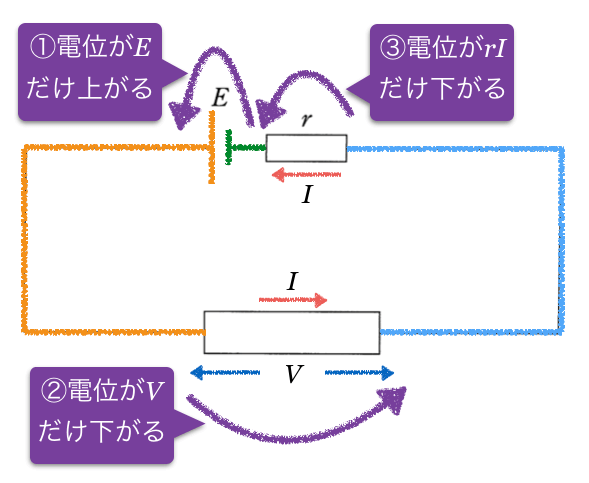
これで元に戻ったので、式を立ててみるわ。電位が0から出発して、電位の上下を考えて、元に戻ったときに電位が0になればいいので、
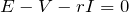
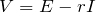

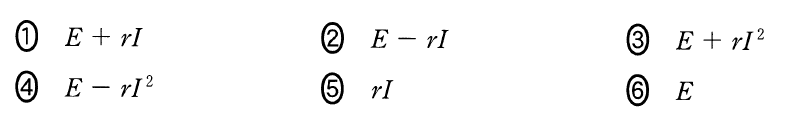

![]() とおいてみたら?
とおいてみたら?
![]() と
と![]() の合成抵抗なので、直列だから
の合成抵抗なので、直列だから![]() ね。流れる電流は
ね。流れる電流は![]() だから、オームの法則より、
だから、オームの法則より、![]()
![]() は与えられていないのと、まだ抵抗Aの両端の電圧
は与えられていないのと、まだ抵抗Aの両端の電圧![]() を使ってないね。
を使ってないね。![]()
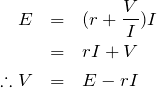
![]() だけ電位が下がる
だけ電位が下がる![]() だけ上げる
だけ上げる
![]() だけ上がって、抵抗Aで電位が
だけ上がって、抵抗Aで電位が![]() だけ下がって、
だけ下がって、
![]() だけ下がるんだけど、もともと抵抗Aの電圧は
だけ下がるんだけど、もともと抵抗Aの電圧は![]() と与えられているから、ここは
と与えられているから、ここは![]() だけ電位が下がる、ということなんだよ。
だけ電位が下がる、ということなんだよ。
![]() というだけでは、どっちの電位が高いのか分からないけど、電流の向きが分かっているじゃない。電流って、必ず電位の高い方から低い方へ流れるんだよ。つまり電流の流れる方へ電位が下がるんだ。
というだけでは、どっちの電位が高いのか分からないけど、電流の向きが分かっているじゃない。電流って、必ず電位の高い方から低い方へ流れるんだよ。つまり電流の流れる方へ電位が下がるんだ。![]() 下がるのね。
下がるのね。
![]()
![]()