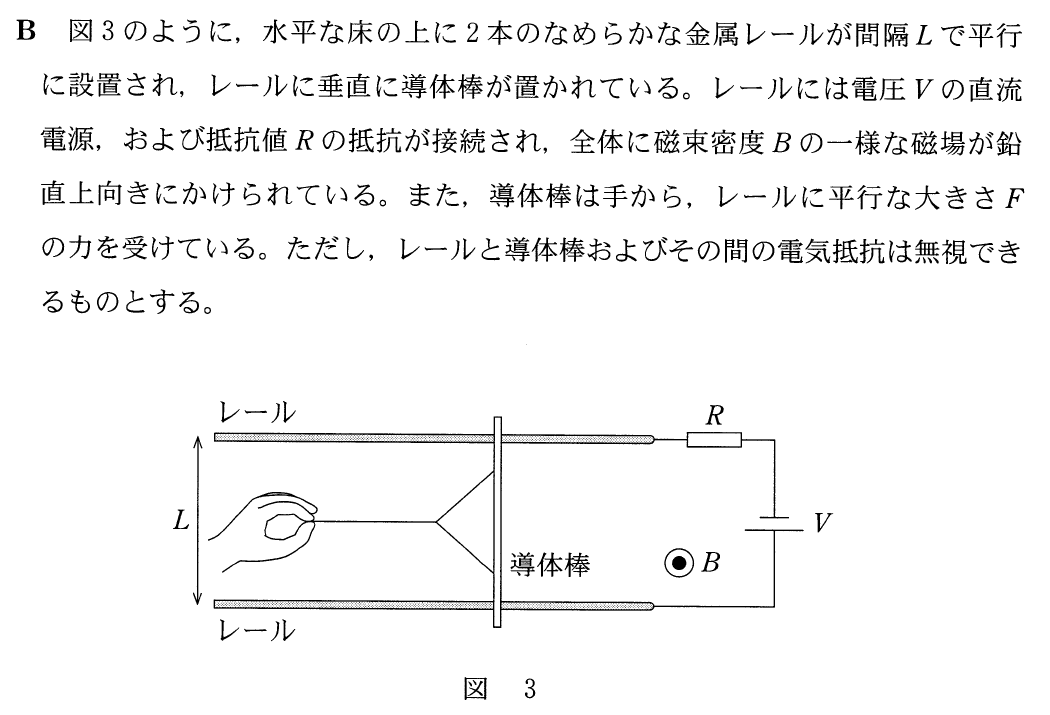
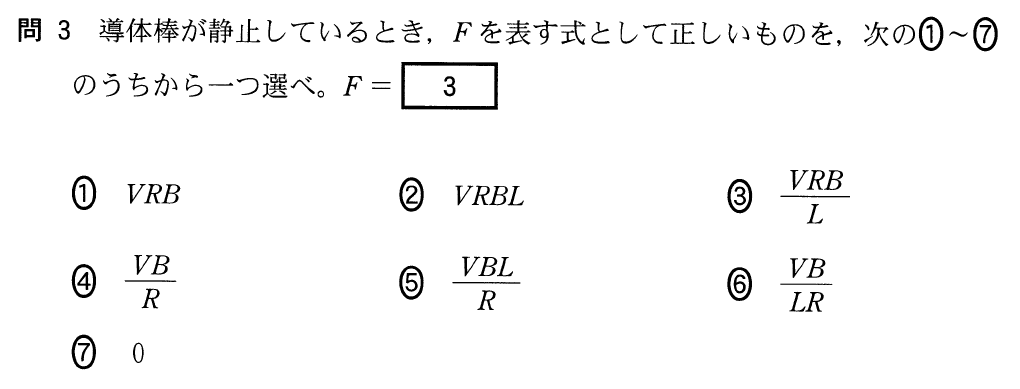
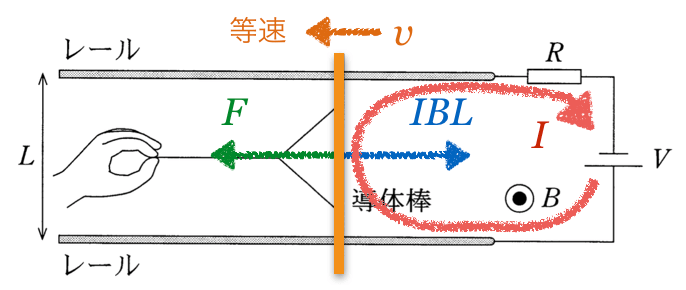
そうだね。図としてはよく見る感じだけど、電源が付いていて、さらに力を加えて導体棒を動かす、と両方あるのは、少し珍しいかもね。でもやることは一緒だね。
そうなのね。じゃあまずは、導体棒が静止しているから力のつりあいの式かな?図の左右方向だけでいいわよね。
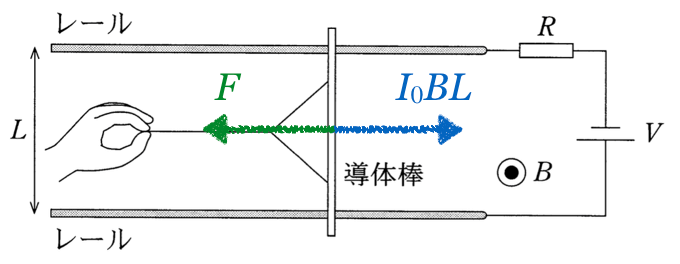
導体棒にはたらく力の矢印を描くと、手が引く力
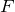
が左向き、それから、右向きは・・・何だろう?
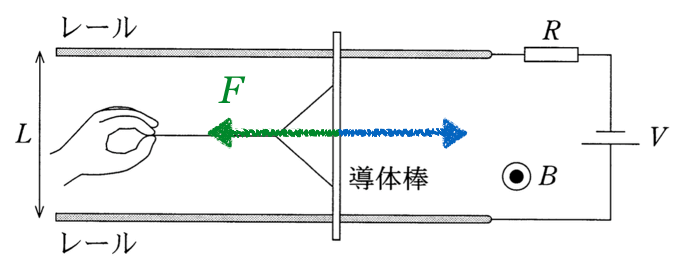
そうか、フレミング左手の法則で向きを求めるやつね。
左手の中指が電流の向きだから図の上向き、人差し指が磁場の向きで紙面に垂直で裏から表の向き、すると親指は・・・ちゃんと右になった!
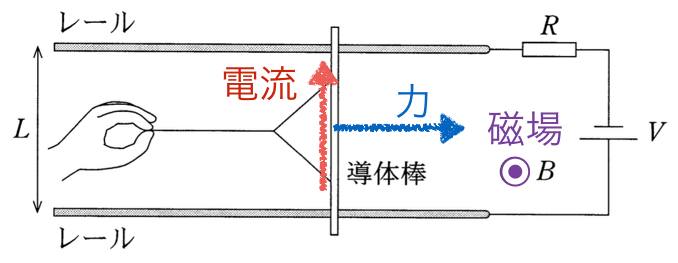
良かった!というわけで、左右方向の力はこの2つだけなので、力のつりあいの式だね。
手で引く左向きの力は
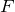
でいいわね。右向きの力は確か
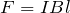
だったかな。
ちゃんと覚えていたね。その中で、
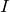
は次の問題で出てくるから、この段階では
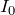
としておこう。
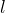
は
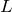
ね。それと、
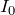
は与えられていないので、何とかしなきゃダメだね。
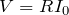
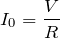
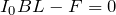
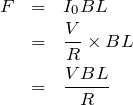
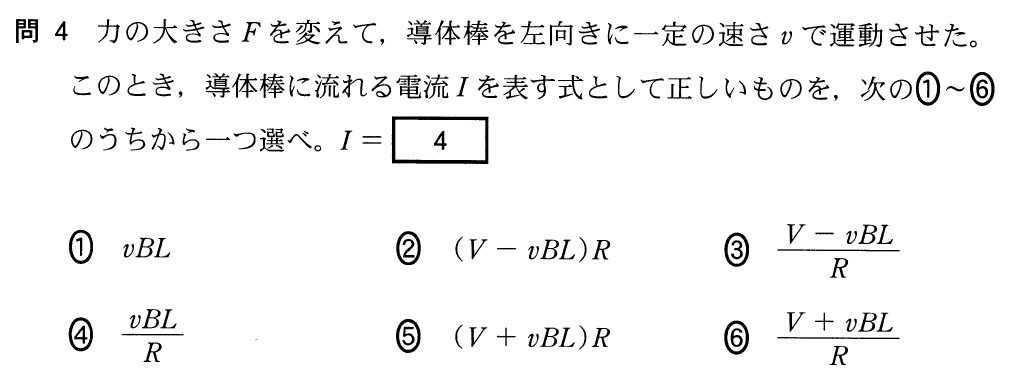
導体棒が動いている場合って、もう電流は問3の
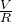
ではないのね?
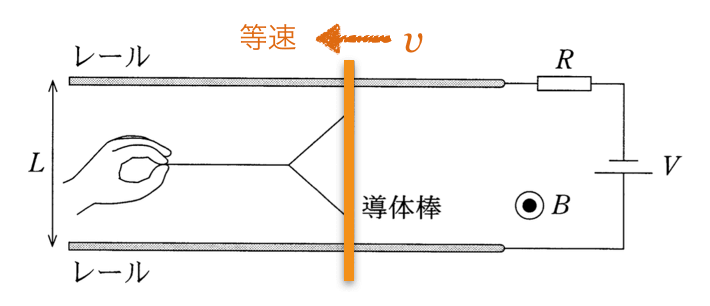
選択肢に無いもんね。磁場の中で導体棒が動くとどうなるか覚えてる?
あ~そういえば、聞いた覚えがある。導体棒が電池になるんだっけ?
確か、
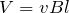
だったかな。すべての選択肢に
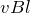
が入ってるもんね。
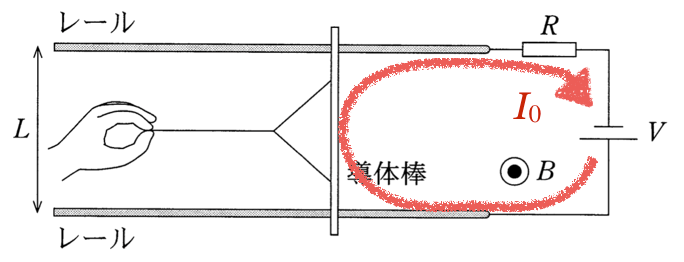
向きの求め方はいくつか方法があるんだけど、今はレンツの法則を使おうかな。導体棒と電源を含めた1巻きコイルだと考えると、導体棒が左に動くことで、このコイルを貫く磁束が増えるよね。
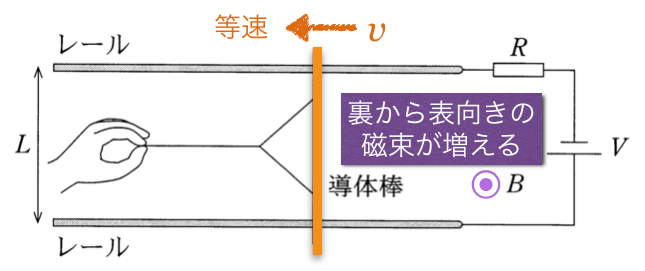
コイルの面積が増えるから、磁束が増えるっていうことね。
磁束の向きは紙面に垂直で裏から表なので、その増加を妨げる向き、つまり紙面に垂直で表から裏の向きに磁束ができるように、コイルに電流を流そうと起電力が生じるんだ。
向きは右ねじの法則に従うから分かるんだ。この図で言うと右回りに電流が流れるように導体棒に起電力が生じるから、上が正極になるような電池だね。
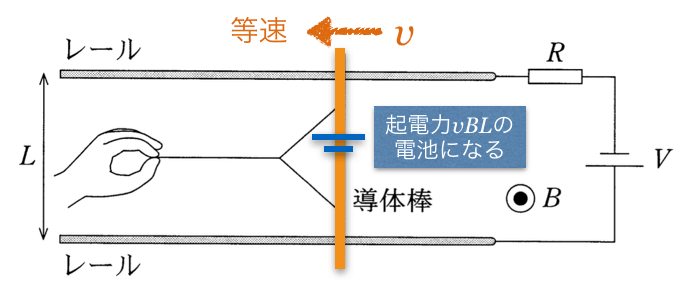
ということは、右にある電源と同じ向きね。電源の直列接続と考えて良いのね。
今後の応用を考えると、キルヒホッフの第2法則を使いたいところだけど、この問題では電源の直列接続で大丈夫だ。
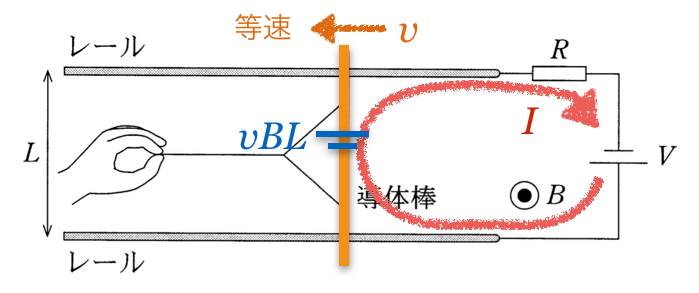
起電力が
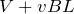
で、抵抗が
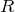
なので、オームの法則から
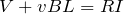
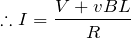
電力の式って
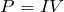
よね。
そうだね。でも気をつけなきゃダメなのは、この式は抵抗を流れる電流
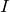
と抵抗にかかる電圧

を使うことなんだ。この問題の

は抵抗にかかる電圧じゃないから、気をつけてね。

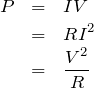
そうだね。まぁいろいろあるけど、すべてオームの法則
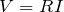
で変形しているだけだから、1つ覚えていれば変形は簡単だよね。じゃあ、今使えるのはどの式かな?
抵抗を流れる電流は
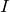
なので、
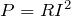
が使えるわよね。あと選択肢を見ると、
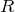
が使われていないので、問4の答えを変形して、

いいところまで来たね。後は、等速なので、左右方向にはたらく力がつりあってるんだよね。
そういうことか。等速ということは、加速していないんだから力がつりあってるんだったわね。
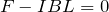
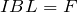
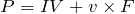
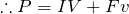
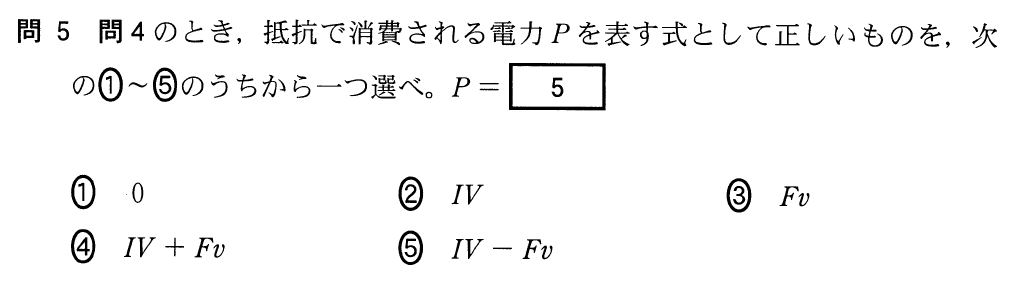
正解!答えは④だね。あらためて答えを見ると、抵抗で消費される電力は、電源で作り出した電力と、手のした仕事率の和になっているね。


![]() が左向き、それから、右向きは・・・何だろう?
が左向き、それから、右向きは・・・何だろう?

![]() でいいわね。右向きの力は確か
でいいわね。右向きの力は確か![]() だったかな。
だったかな。![]() は次の問題で出てくるから、この段階では
は次の問題で出てくるから、この段階では![]() としておこう。
としておこう。![]() は
は![]() ね。それと、
ね。それと、![]() は与えられていないので、何とかしなきゃダメだね。
は与えられていないので、何とかしなきゃダメだね。

![]()
![]()
![]()
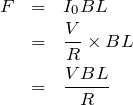

![]() ではないのね?
ではないのね?
![]() だったかな。すべての選択肢に
だったかな。すべての選択肢に![]() が入ってるもんね。
が入ってるもんね。


![]() で、抵抗が
で、抵抗が![]() なので、オームの法則から
なので、オームの法則から![]()
![]()

![]() よね。
よね。![]() と抵抗にかかる電圧
と抵抗にかかる電圧![]() を使うことなんだ。この問題の
を使うことなんだ。この問題の![]() は抵抗にかかる電圧じゃないから、気をつけてね。
は抵抗にかかる電圧じゃないから、気をつけてね。
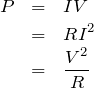
![]() で変形しているだけだから、1つ覚えていれば変形は簡単だよね。じゃあ、今使えるのはどの式かな?
で変形しているだけだから、1つ覚えていれば変形は簡単だよね。じゃあ、今使えるのはどの式かな?![]() なので、
なので、![]() が使えるわよね。あと選択肢を見ると、
が使えるわよね。あと選択肢を見ると、![]() が使われていないので、問4の答えを変形して、
が使われていないので、問4の答えを変形して、![]()
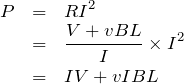

![]()
![]()
![]()
![]()


コメント
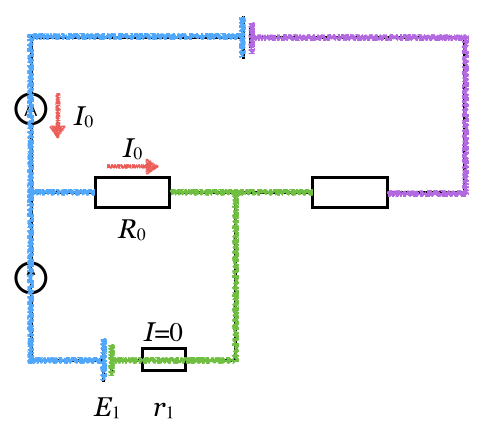
[…] 2016年度追試第2問B「磁場中を動く導体棒」 […]