■導線がつながっていれば等電位
電位のグラフを選ぶ問題ね。どうも電位って苦手なのよね。
それほど難しくはないんだけどね。このグラフもよく教科書に載っているんだよね。
似たようなのがいっぱいあって,どれがどれだか分からなくなるのよ。
確かに似たようなのがあるけど,基本をきちんと押さえていれば,ちゃんとグラフを選べるよ。
まず,この問題のような電気回路での電位の考え方が大切なんだ。

金属球とか,金属の板とかひとかたまりの導体はどこも等電位なんだけど,そこに導線がつながっていたりしても,つながっている部分は全て等電位になるっていうことなんだ。
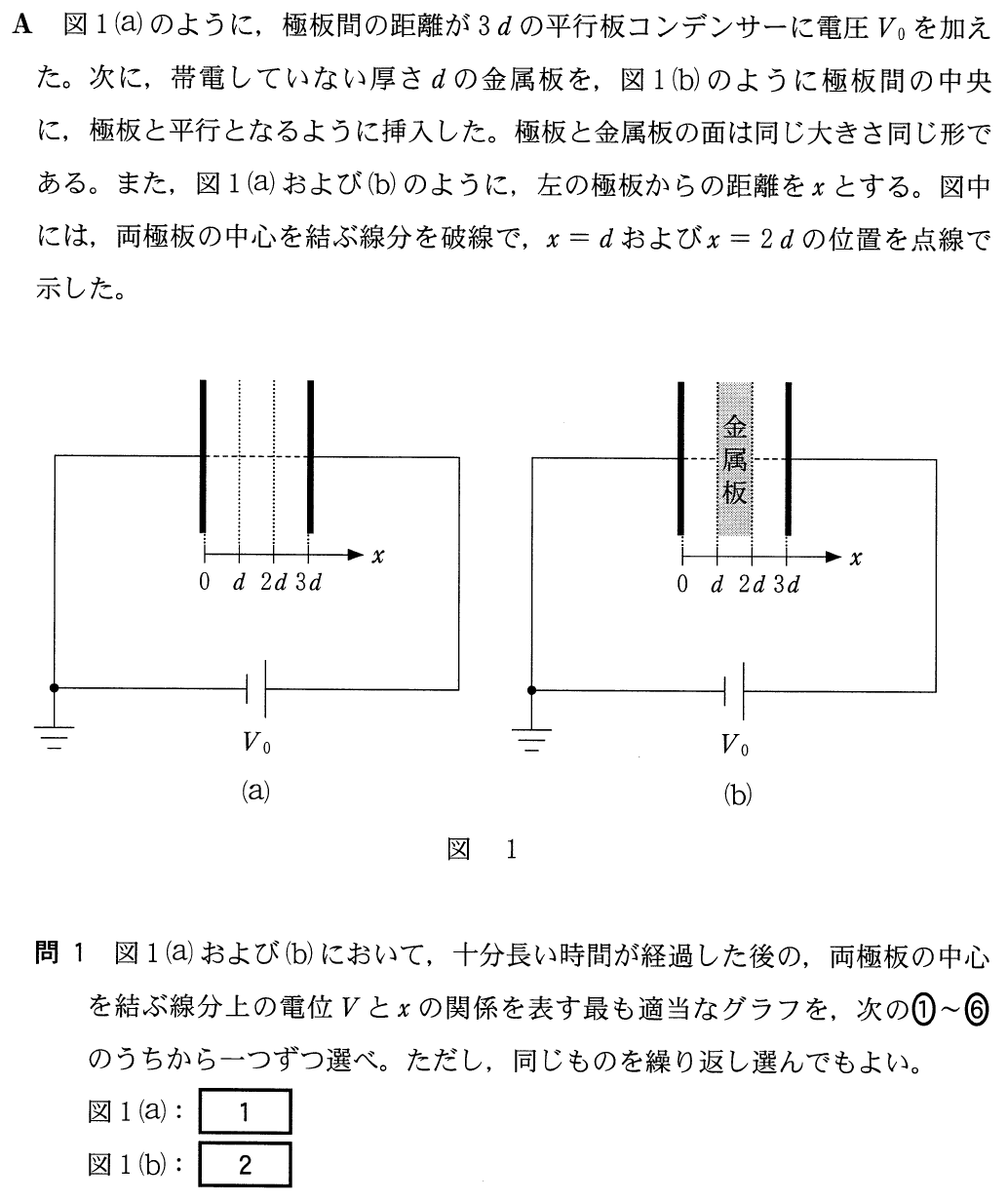
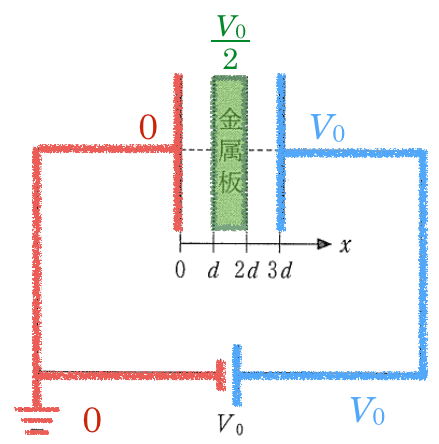
(a)の回路図を見てみると,まず左下のマークが接地とかアースといって,電位が0であることを表しているんだ。
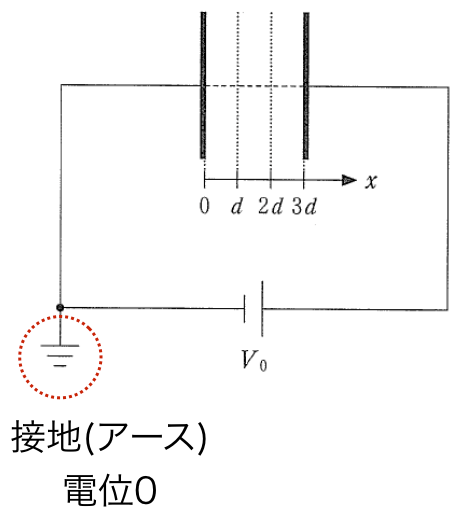
すると,このアースとつながっている導体は全て電位が0ということなんだ。
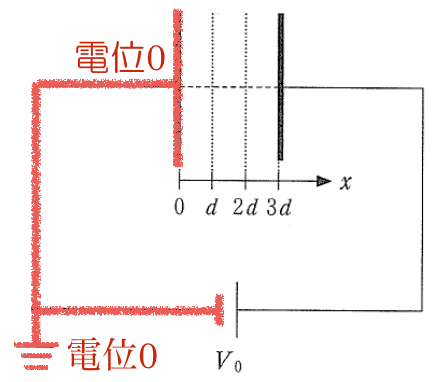
電池の負極もつながっているので電位が0になるのね。
そうだよ。電池の電圧が
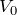
というのは,
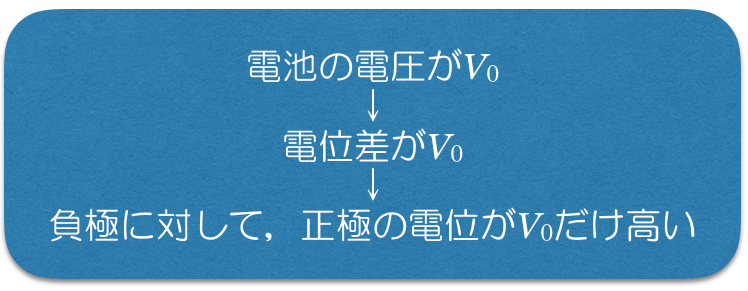
ということなので,電池の正極と,そこにつながっている部分の電位は全て
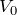
になるんだ。
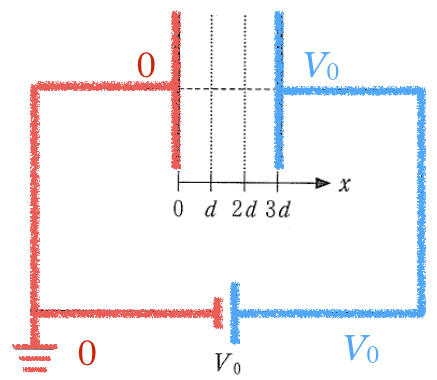
なるほど。ということは,左の電極の電位は0で,右の電極の電位は
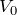
ね。
■一様な電場と電位の関係
もう一つ,よく出てくる基本的な考え方を使うんだ。一様な電場と電位の関係だ。
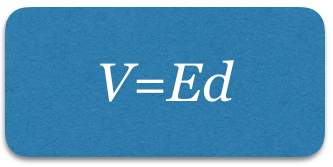
この式は一様な電場
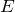
のときに使えるんだ。この問題のように,2枚の極板に挟まれているところは,一様な電場と考えていいんだ。
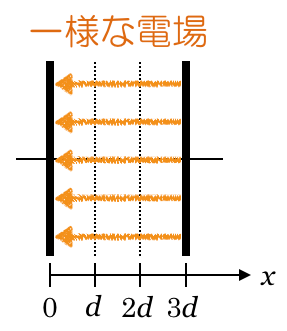
ということは,この

=
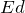
という式が使えるのね。
そうなんだ。つまり,この

=
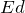
が使えるということは,
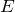
は一定なので,

と
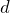
は比例関係ということなんだ。
■金属板を入れても極板の電位は変わらない
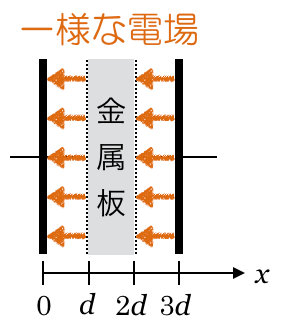
その通りだ。それじゃあ,極板間に金属板が入っているとどうなるだろう?
さっきと同じように考えると,左の極板の電位が0で,右の極板の電位が
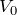
というのは,変わらないんじゃない?
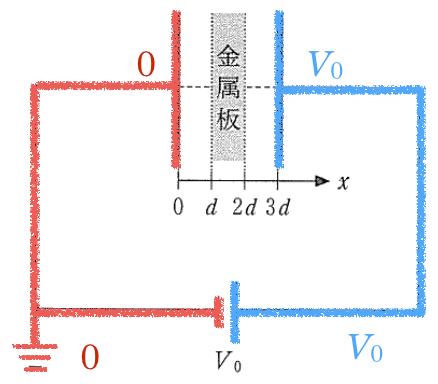
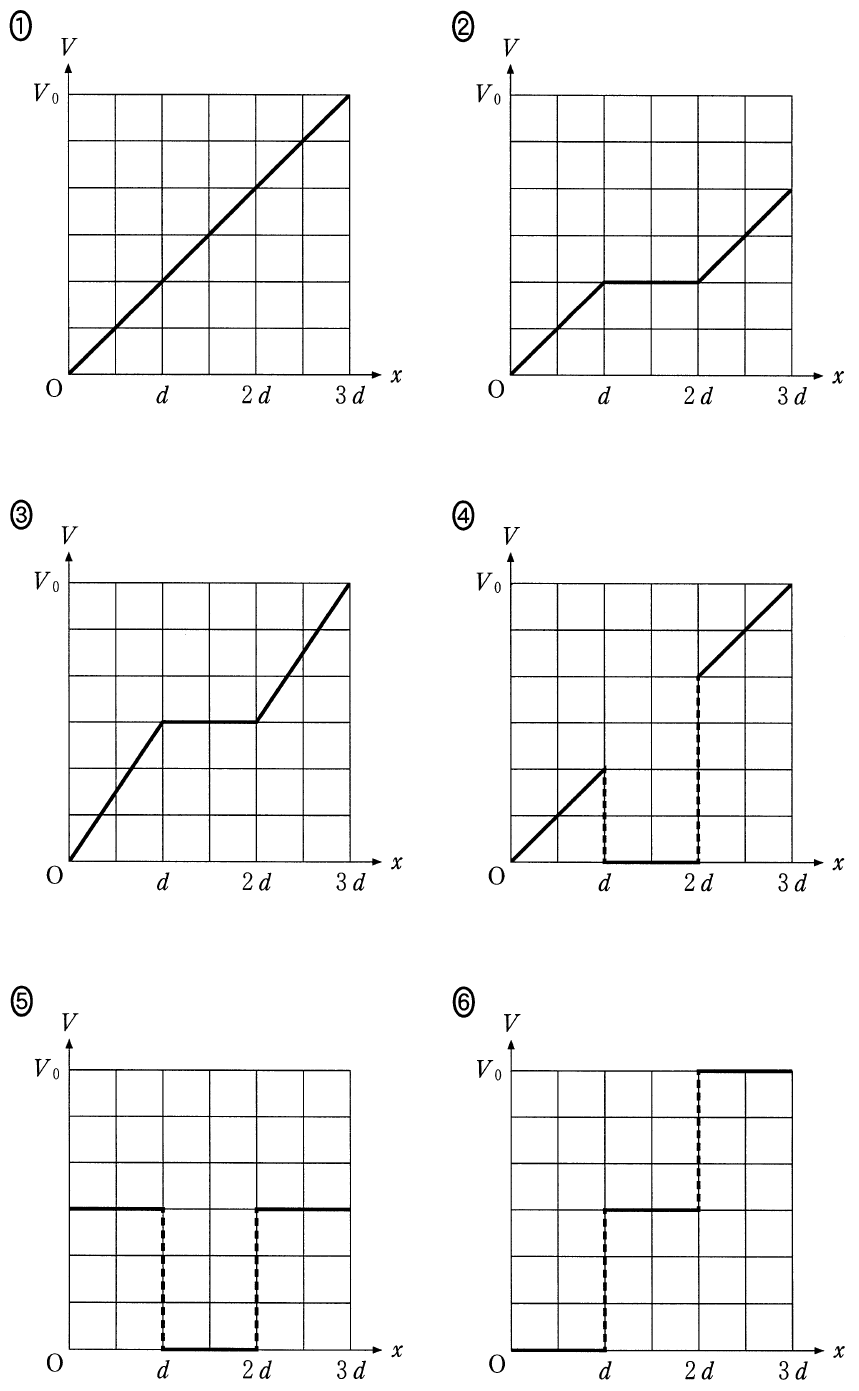
そうなんだよ。変わらないんだよ。なので,この段階では(a)のときと同じで,グラフは①,③,④,⑥のうちのどれかなんだ。
さっきやったけど,導体は全て等電位なんだよ。つまり,

=
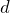
から

=
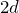
までは電位は変化しないんだ。
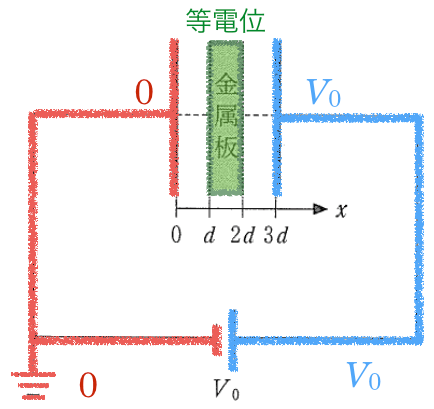
そうだね。この金属板は2枚の極板のちょうど真ん中に入っているので,電位もちょうど中間になるんだよ。
電位が中間ということは金属板の電位は
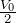
?
極板と金属板の間には,(a)と同様に一様な電場ができているんだ。
ということは,

=
が成り立つから,⑥のような階段状ではないわね。
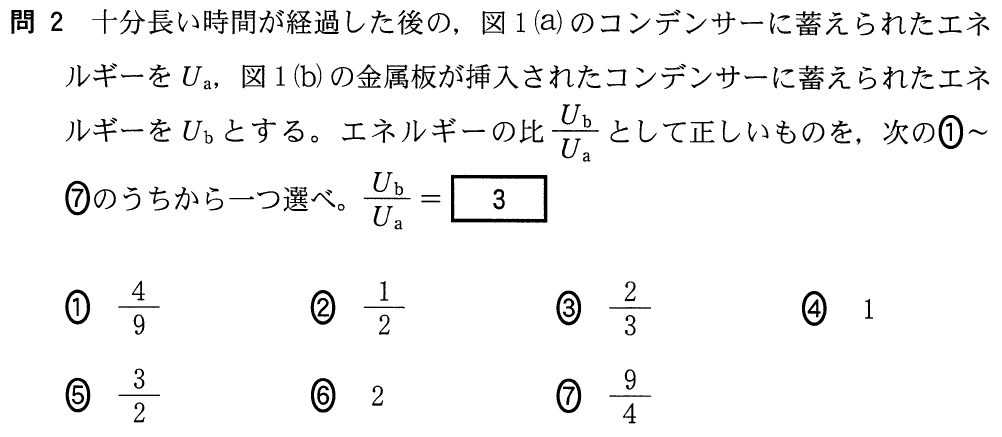
■コンデンサーに蓄えられたエネルギー
コンデンサーに蓄えられたエネルギーの式って,確かあったわよね。式が長かった記憶がある。
長くなんかないよ。きっと変形した分も合わせて,長いと思ってるんだよ。こうだよ。
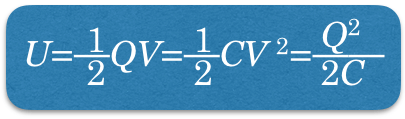
長く見えるけど,コンデンサーの問題でよく使う
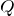
=
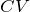
という式で変形しているだけだよ。
そうなの?どれか1つだけ覚えれば,あとは変形するだけなの?
そうなんだよ。今この問題では,金属板を入れても入れなくても,極板間の電圧は
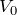
なのと,いずれにせよ電気容量
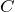
を求めなきゃダメなので,
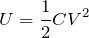
なるほど,ちょっとできそう。(a)と(b)のコンデンサーの電気容量をそれぞれ
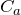
,
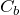
とすると,
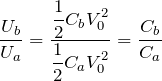
いいね。結局はエネルギーの比は電気容量の比になるということだよね。
■電気容量と極板間距離の関係
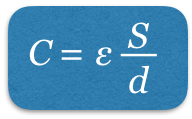
まず(a)の方は簡単で,極板の面積を
とすると,
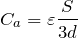
金属板については,2通りのやり方があって,今は両方やってみようか。まずは金属板を極板と考える方法だ。
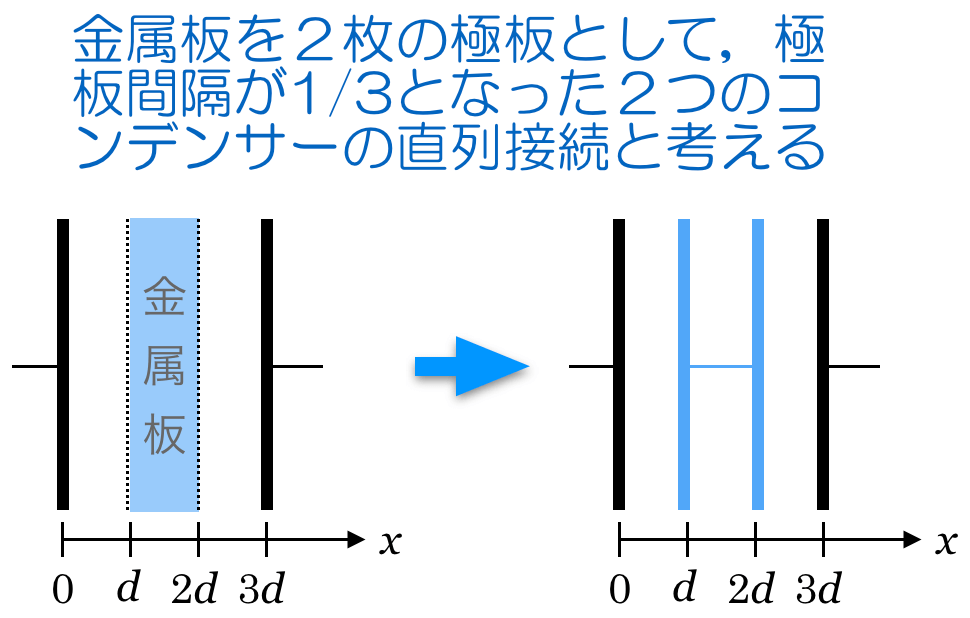
■コンデンサーの直列接続
2つのコンデンサーの合成容量は,直列接続と並列接続でこんな関係だったよね。

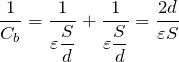
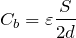
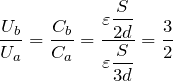
■電気容量は金属板をどこに入れても同じ
もう一つの方法でもやっておこう。2枚の極板の間に金属板を挿入した場合の電気容量は,金属板をどの場所に入れても同じなんだ。
金属板を真ん中に入れても,左右どちらかに寄っていても同じっていうこと?
そうなんだよ。さっきのやり方だと,金属板は真ん中にあるということで,2つのコンデンサーの直列接続だ,と考えたけど,金属板を例えば右側に寄せちゃうと簡単になるね。
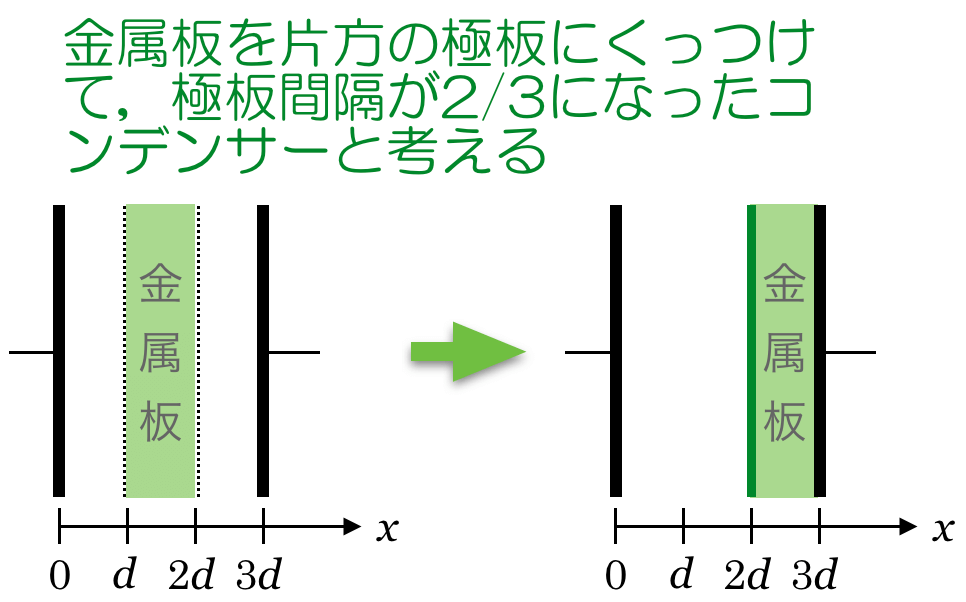
そうだよ。この問題の場合は,極板間隔が
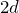
になったと考えられるね。
さっきはコンデンサーの直列接続の式を使って,分数のややこしい計算をして
を求めたけど,これだと計算しなくても求まるじゃない!
簡単に同じ答えになるでしょ。このポイントは覚えておいたほうがいいね。






![]() というのは,
というのは,
![]() になるんだ。
になるんだ。
![]() ね。
ね。![]() =
=![]() で
で![]() ,
,![]() =
=![]() で
で![]() のグラフを選べばいいんだ。
のグラフを選べばいいんだ。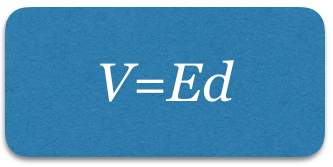
![]() のときに使えるんだ。この問題のように,2枚の極板に挟まれているところは,一様な電場と考えていいんだ。
のときに使えるんだ。この問題のように,2枚の極板に挟まれているところは,一様な電場と考えていいんだ。
![]() =
=![]() という式が使えるのね。
という式が使えるのね。![]() =
=![]() が使えるということは,
が使えるということは,![]() は一定なので,
は一定なので,![]() と
と![]() は比例関係ということなんだ。
は比例関係ということなんだ。![]() というのは,変わらないんじゃない?
というのは,変わらないんじゃない?
![]() =
=![]() から
から![]() =
=![]() までは電位は変化しないんだ。
までは電位は変化しないんだ。
![]() ?
?

![]() =
=![]() が成り立つから,⑥のような階段状ではないわね。
が成り立つから,⑥のような階段状ではないわね。
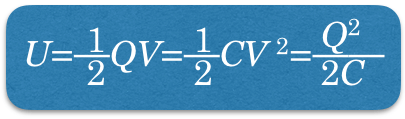
![]() =
=![]() という式で変形しているだけだよ。
という式で変形しているだけだよ。![]() なのと,いずれにせよ電気容量
なのと,いずれにせよ電気容量![]() を求めなきゃダメなので,
を求めなきゃダメなので,![]()
![]() ,
,![]() とすると,
とすると,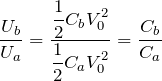
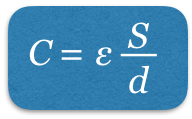
![]() とすると,
とすると,![]()


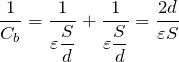
![]()
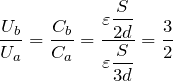

![]() になったと考えられるね。
になったと考えられるね。![]()
![]() を求めたけど,これだと計算しなくても求まるじゃない!
を求めたけど,これだと計算しなくても求まるじゃない!