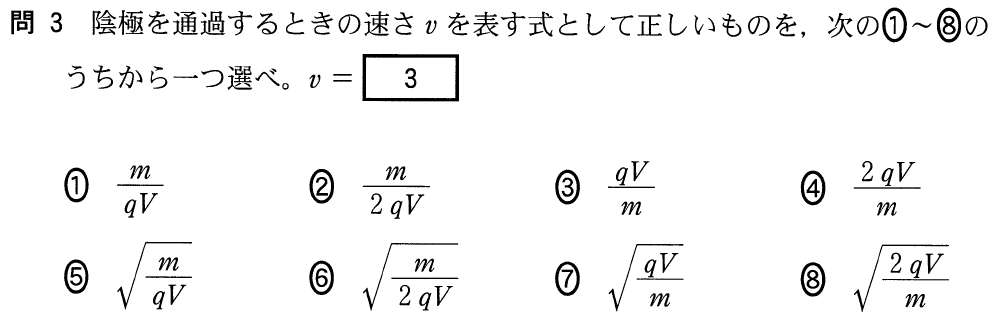
■電場(電界)の向きと力
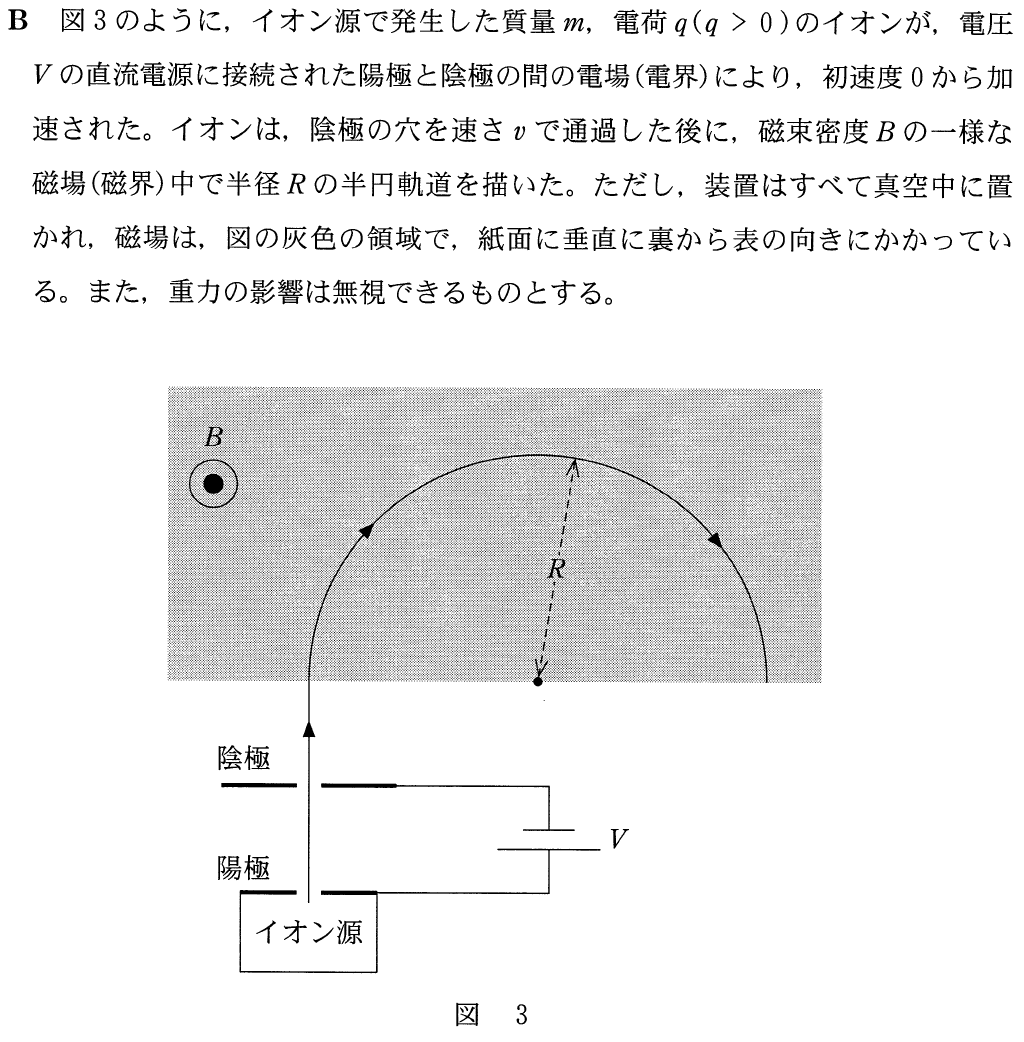
イオンが陰極を通過するときの速さを求めるんだから,上半分の磁場の部分は関係ないわよね。
図の下にある「イオン源」って何?そこからイオンが出てくるっていうこと?
そういうことだね。ただ化学では,イオンは通常水溶液中や,結晶中にあるものを扱うけど,この問いでは真空中にイオンを放出するので,化学とはちょっと違う方法でイオンを生成するんだ。でも生成方法が違ってもイオンはイオンだよ。
ふーん,そうなんだ。じゃあ,イオン源からイオンが飛び出るとして,その先がよく分からないわ。
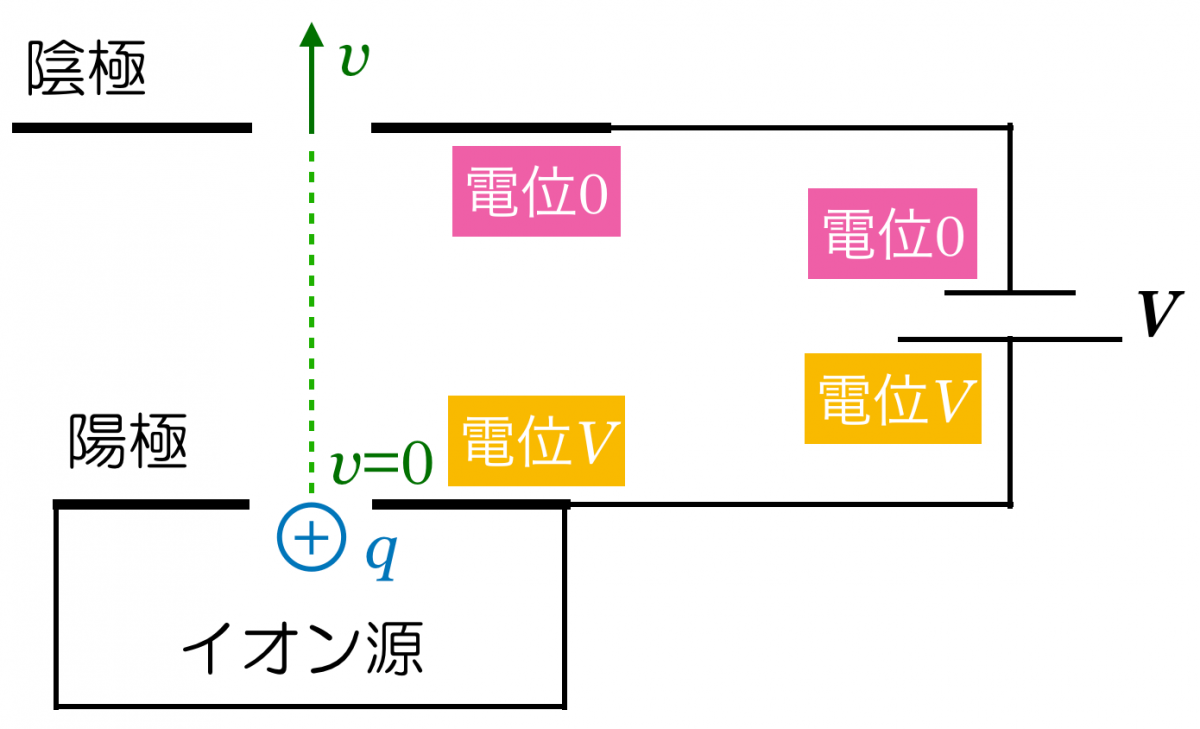
飛び出るといっても,問題文にある通り,初速度は0だけどね。次に大切なのは,「陽極」,「陰極」だね。これも問題文にあるけど,陽極と陰極の間には電場(電界)ができるんだ。電場の向きは分かるかな?
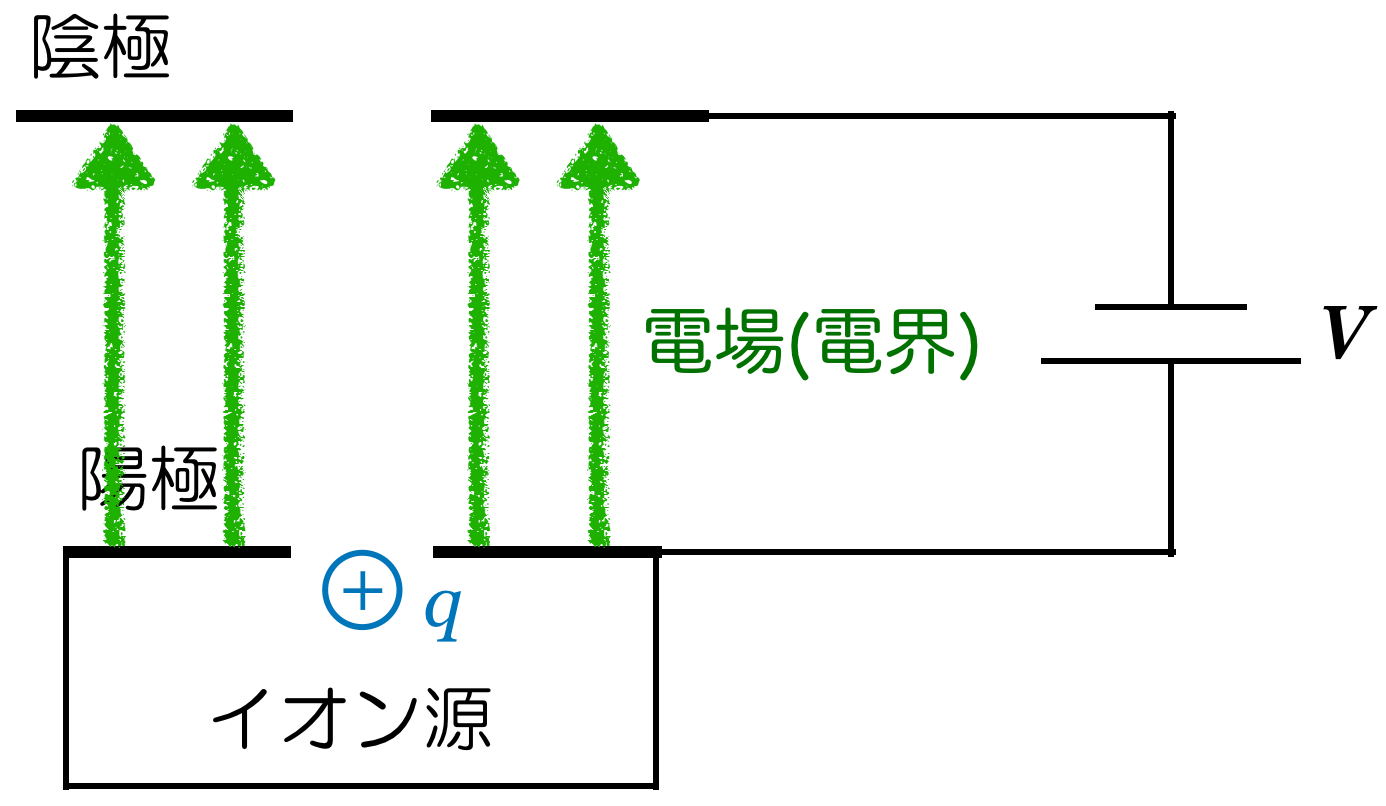
そうだね。ということは,そこにイオンが入ってくると,力を受けるんだけど,力の向きは分かるかな?
確か,プラスの電荷は電場の向きに力を受けて,マイナスの電荷は電場の向きと逆向きに力を受けるのよね。
今は電荷
なので,電場の向きに力を受けるのね。
じゃあ,加速度を求めて等加速度直線運動の式に入れれば,求めたい速さが求まるわね。
そうだね。その考え方は合ってるんだけど,この問いの条件設定では,ちょっと面倒くさいんだよね。陰極と陽極の間隔を
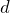
と置いて,電場の強さ,イオンが受ける力の大きさ,イオンの加速度を順に求めて,等加速度直線運動の式に入れれば答えは出るんだけどね。
順番に出していけば答えにはたどり着くので,簡単な方法を思いつかなければ,やるべきだと思うよ。
簡単な方法を思いつかないわ。でも簡単な方法を教えてよ。
■電位と静電気力による位置エネルギー
そうか。ヒントとしては,エネルギーを考えるんだけど。
とりあえず求めたいのは陰極を通過するときの速さだから,

とするわね。
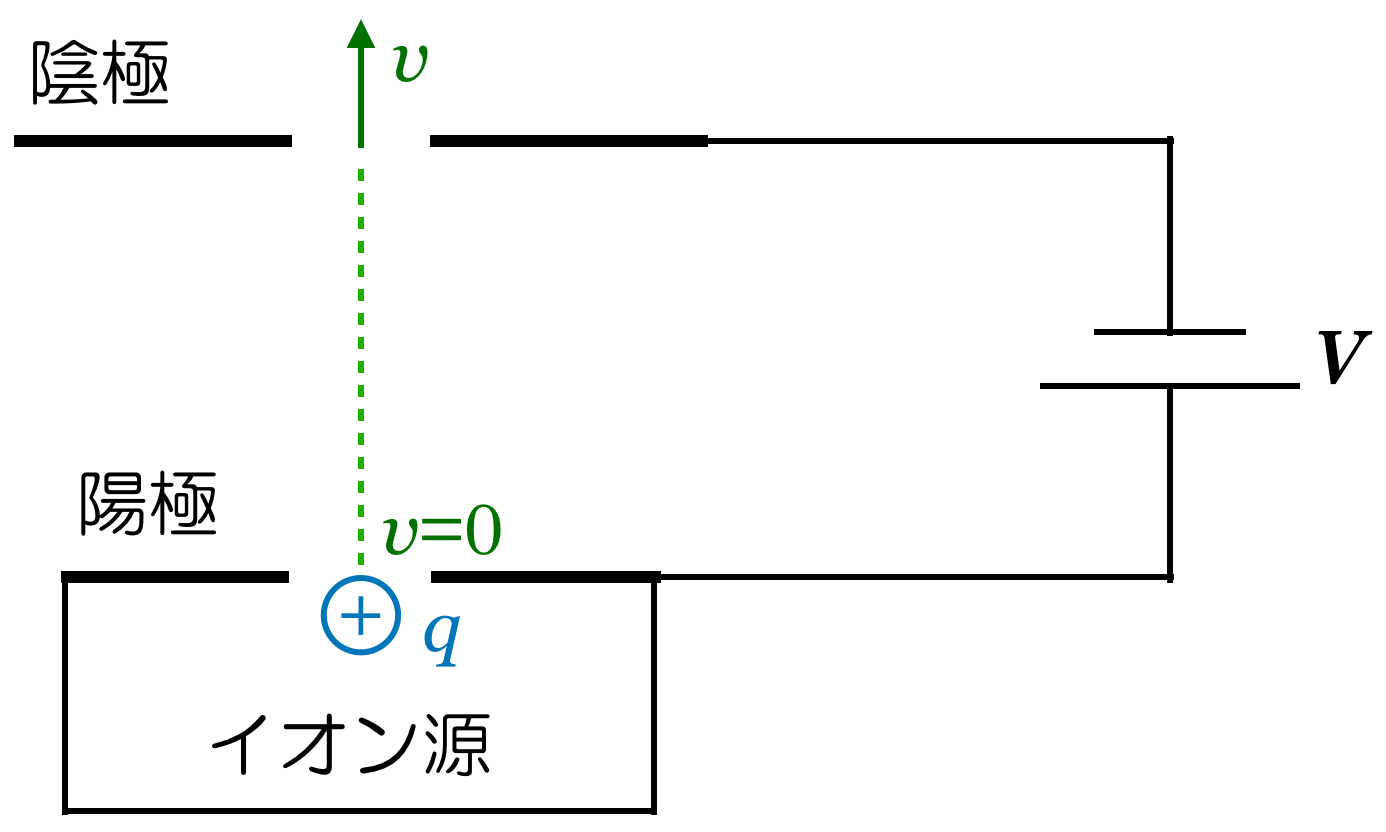
そうすると,運動エネルギーを考えることはできるね。
こういう場合には,静電気力による位置エネルギーを考えるんだ。

この式で大切なのが,

が電圧じゃなくて,電位を表していることなんだ。
電位の考え方って,分かりにくいこともあるけど,この場合はそんなに難しくはないよ。問題の図では電位の基準が決められていないので,電池の負極を電位0としよう。
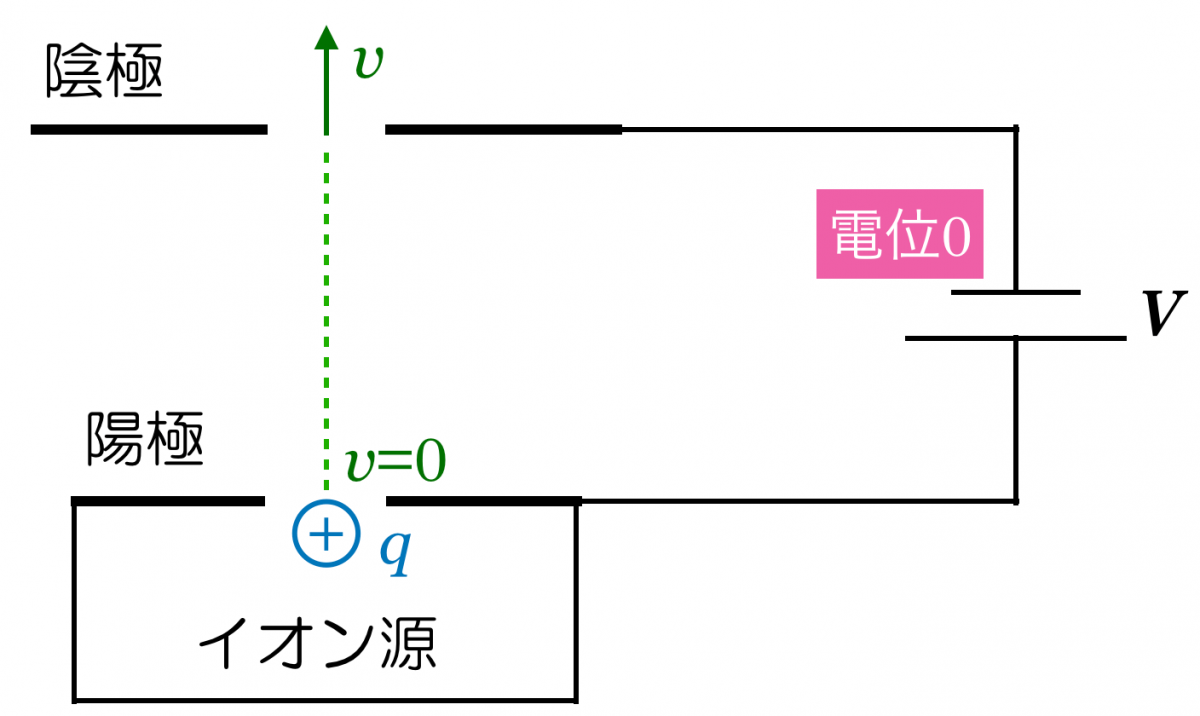
問題文中で規定されていなければ,自分で決めていいんだ。重力による位置エネルギーの基準と一緒だね。そうすると,電池の正極の電位は

になるんだ。
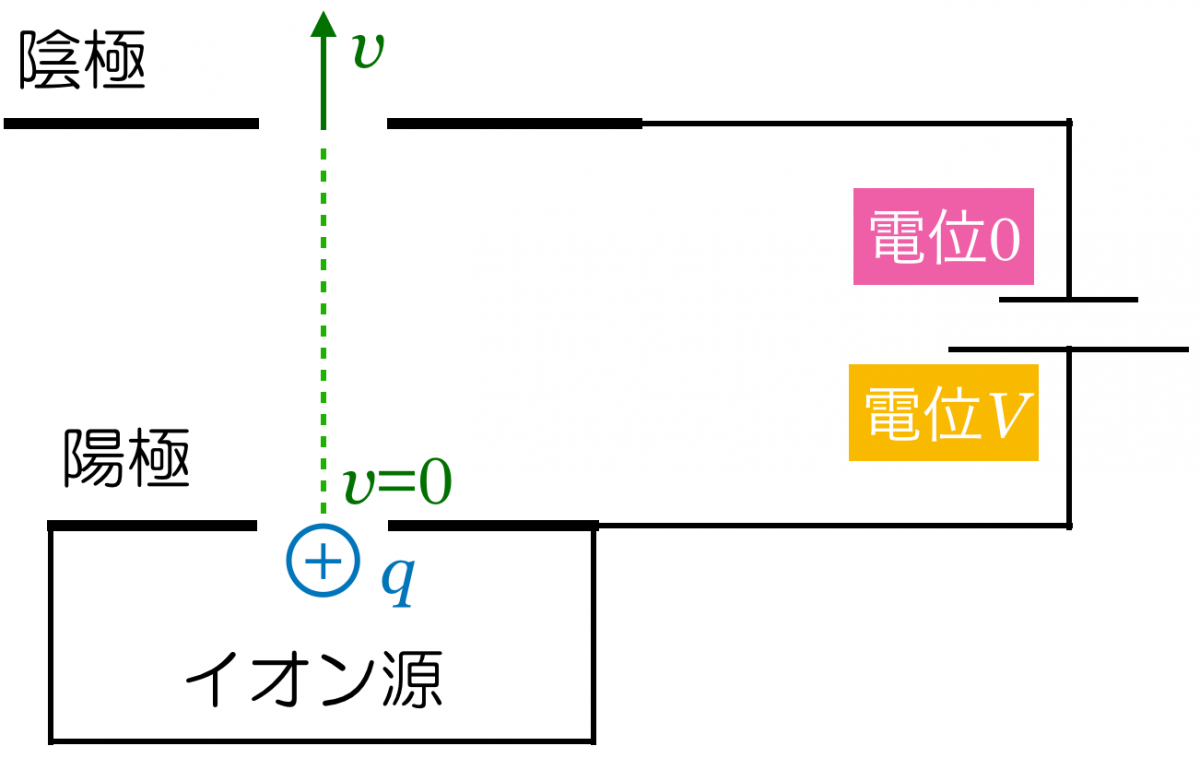
電池の電圧が

だから?
そういうことだよ。電圧が

の電池って負極に対して正極の電位を

だけ上げる道具なんだ。
そうすると,電池の負極とつながっている陰極の電位は0になり,電池の正極とつながっている陽極の電位は

となるんだ。
これで,さっきの静電気による位置エネルギーの式を使うの?
その通りだ。それじゃあ,エネルギー保存の式を立ててみよう。

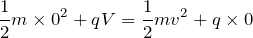
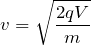
■円運動をする理由
問3で

を求めたけど,問4の選択肢を見ると,

が使われているので,イオンが磁場に速さ

で入るところから考えればいいね。
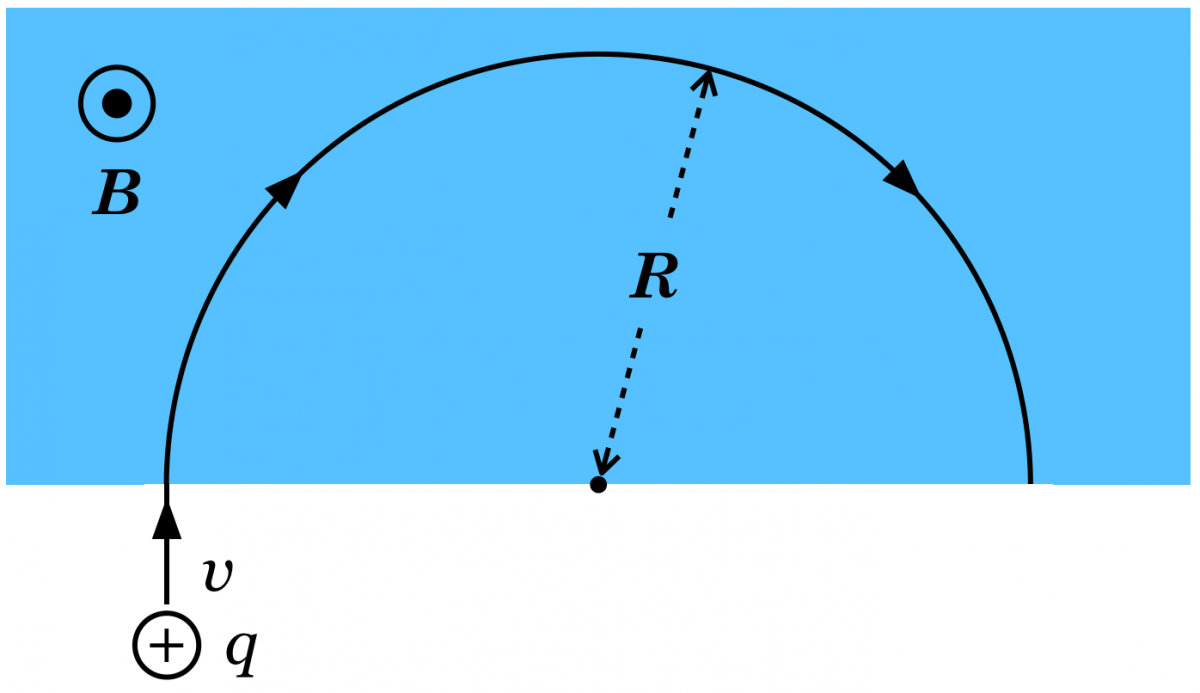
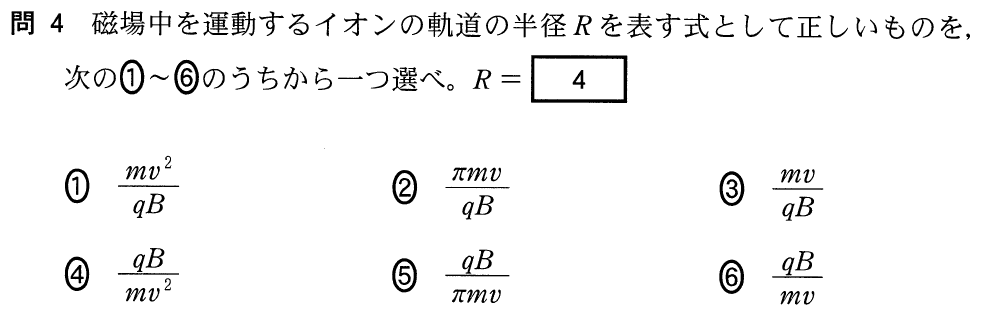
選択肢も見ておくことが大切ね。そこまではいいんだけど,軌道の半径を求めるってどういうこと?
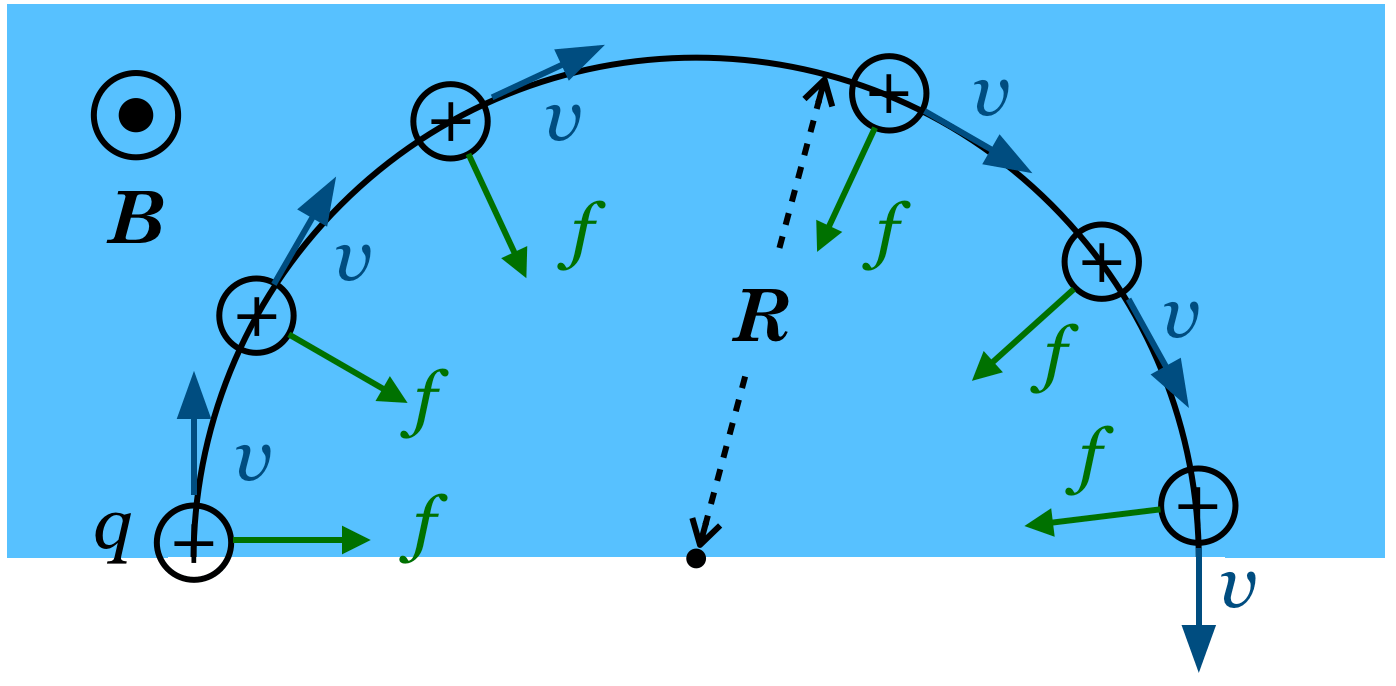
問題文にあるけど,この軌道は「半円軌道」なんだよ。イオンは磁場に入ると円運動をするんだね。なぜ円運動になるか分かる?
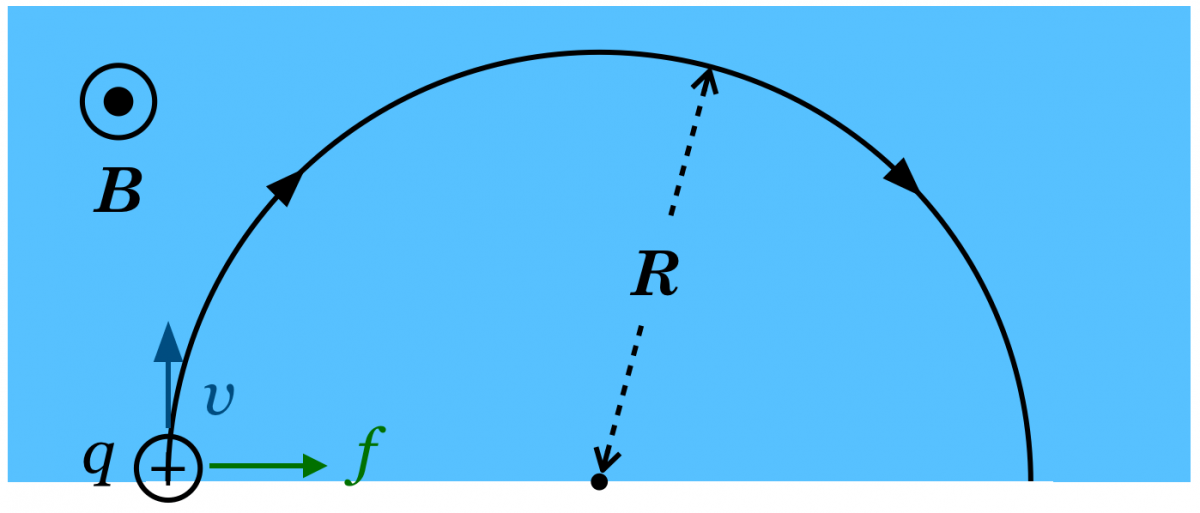
磁場中を運動する荷電粒子には,ローレンツ力という力がはたらくんだ。この問いでは正電荷を持ったイオンなので,速度の向きを電流の向きと考えて,フレミング左手の法則で力の向きが分かるんだ。
ということは,速度の向きが電流の向きで,磁場の向きが紙面の裏から表なので・・・力の向きは右向きね。
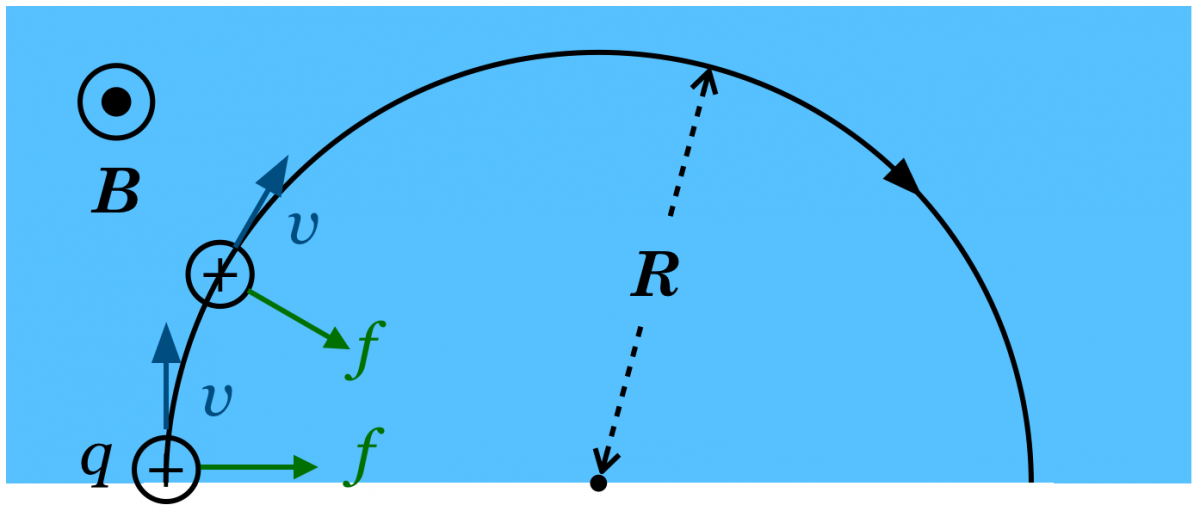
荷電粒子の電荷が負の場合は,電流の向きを逆と考えればいいの?
そういうことだ。今の場合は電荷は右向きの力を受けるので,起動が少し右を向くよね。そうすると,同じように考えると力の向きも少し変わるんだ。
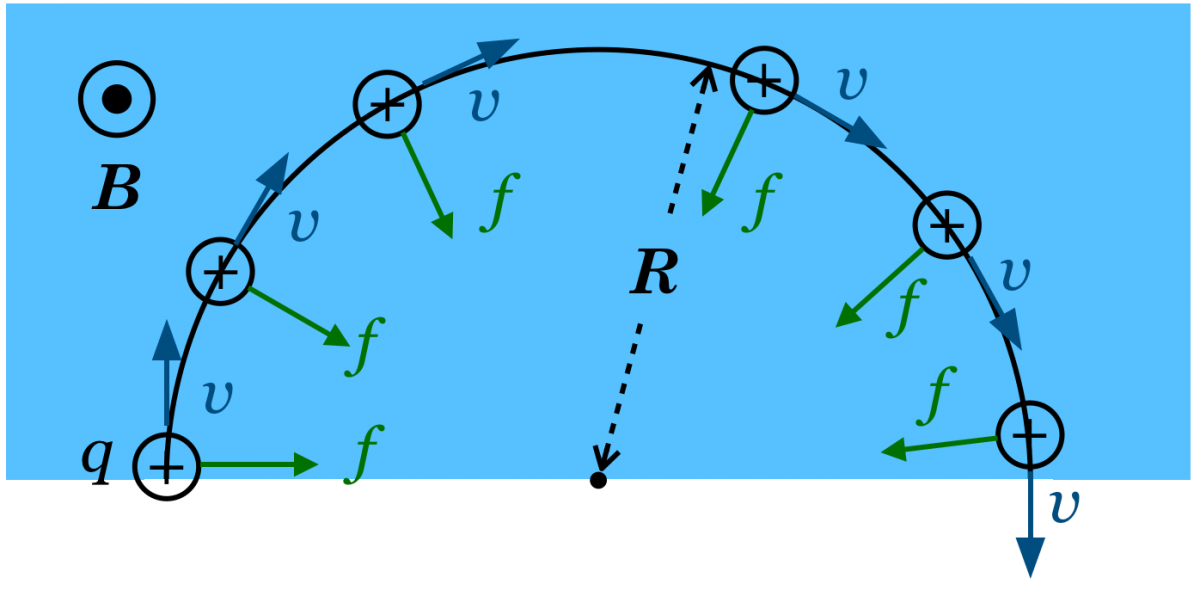
そうなんだよ。つまり,速度の向きと力の向きは常に直角なんだよね。ローレンツ力はどの場所でも1つの点の方向を向いているので,これが向心力となってイオンは円運動をするんだ。
■ローレンツ力と円運動の運動方程式
なんとなく円運動をすることは分かったわ。この円運動の半径を求めるにはどうすればいいの?
半径をすぐに求めようとするよりは,円運動をしているんだから,運動方程式を立ててみよう,ということだな。
確かに円運動をしている場合は,運動方程式を立てることが多い感じがするわ。
円運動って,そもそも円の中心向きに「向心加速度」を持つ加速度運動だから,運動方程式を立てるのが自然なんだ。立ててみようか。
運動方程式だから,
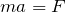
ね。質量は
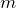
でいいわね。加速度は?

そうだね。今は

が分かっているから,最後の項を使うよね。
あとは力
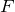
ね。ローレンツ力を入れればいいの?
そうだね。イオンにはローレンツ力しかはたらいていないし,今はそれが向心力になっているから,そのままローレンツ力を入れよう。ちなみにローレンツ力はこんな式で表されるよ。
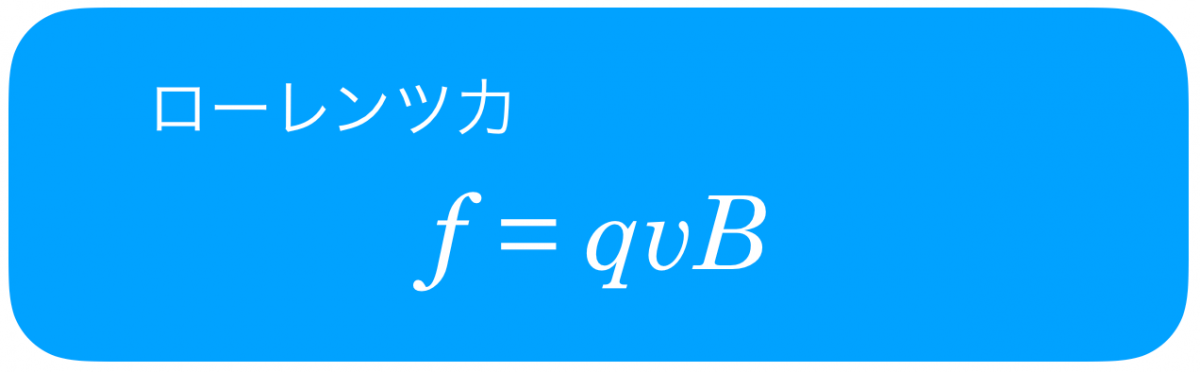
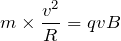
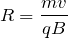



![]() なので,電場の向きに力を受けるのね。
なので,電場の向きに力を受けるのね。
![]() と置いて,電場の強さ,イオンが受ける力の大きさ,イオンの加速度を順に求めて,等加速度直線運動の式に入れれば答えは出るんだけどね。
と置いて,電場の強さ,イオンが受ける力の大きさ,イオンの加速度を順に求めて,等加速度直線運動の式に入れれば答えは出るんだけどね。![]() とするわね。
とするわね。

![]() が電圧じゃなくて,電位を表していることなんだ。
が電圧じゃなくて,電位を表していることなんだ。
![]() になるんだ。
になるんだ。
![]() だから?
だから?![]() の電池って負極に対して正極の電位を
の電池って負極に対して正極の電位を![]() だけ上げる道具なんだ。
だけ上げる道具なんだ。![]() となるんだ。
となるんだ。

![]()
![]()

![]() を求めたけど,問4の選択肢を見ると,
を求めたけど,問4の選択肢を見ると,![]() が使われているので,イオンが磁場に速さ
が使われているので,イオンが磁場に速さ![]() で入るところから考えればいいね。
で入るところから考えればいいね。



![]() ね。質量は
ね。質量は![]() でいいわね。加速度は?
でいいわね。加速度は?
![]() が分かっているから,最後の項を使うよね。
が分かっているから,最後の項を使うよね。![]() ね。ローレンツ力を入れればいいの?
ね。ローレンツ力を入れればいいの?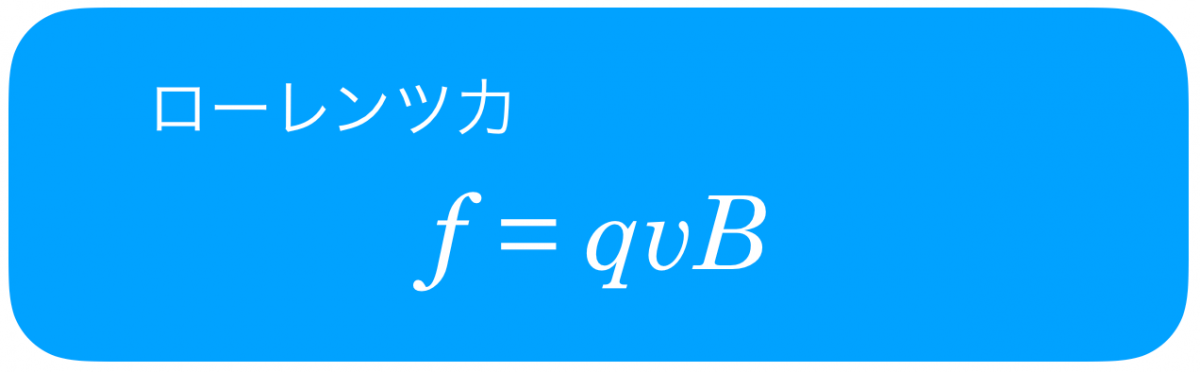
![]()
![]()