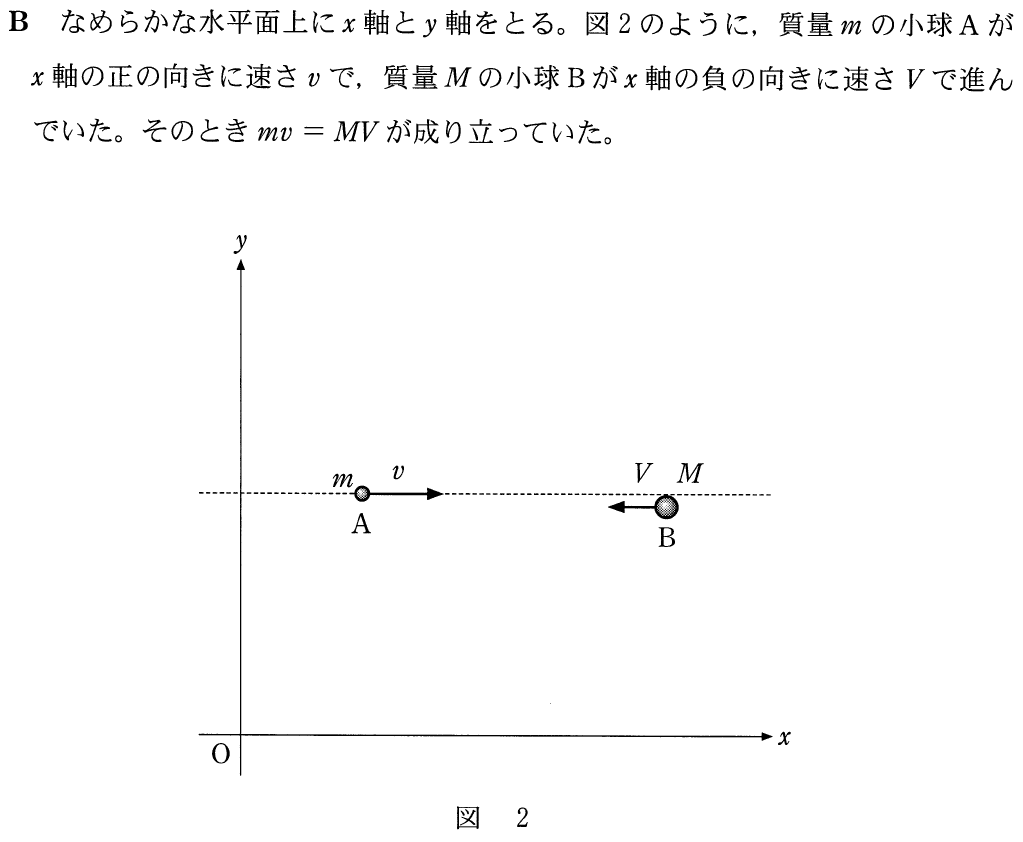

■エネルギーは向きを持たない
運動エネルギーの比を求める問題ね。単純に運動エネルギーを計算すれば良いわよね。
そうだね。強いていえば,エネルギーは向きを持たないスカラーなので,速度の正の向き,負の向き関係なく式を立てればいいね。問題と同じ図だけど,小球に色を付けておくよ。
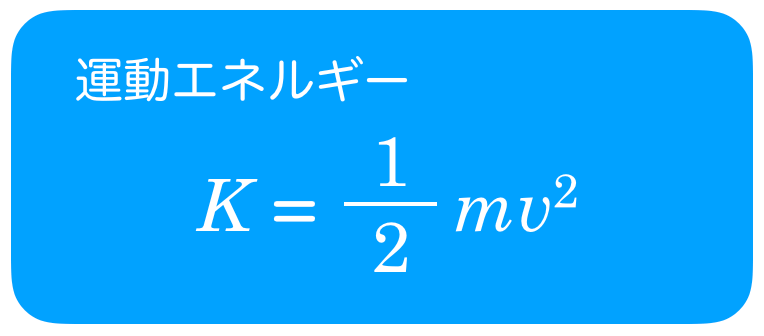
小球AとBの運動エネルギー
と
は,
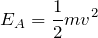
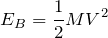
よって,
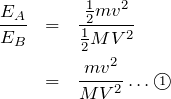
これ以上計算ができないけど,選択肢に答えがないわね。
そうか。
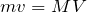
ってやつね。
その式を使って,文字を消去すればいいね。上手い方法もあるけど,今は単純に

を消去しようか。
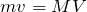
より,
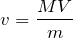
を①に代入して,
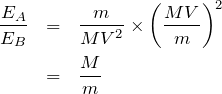
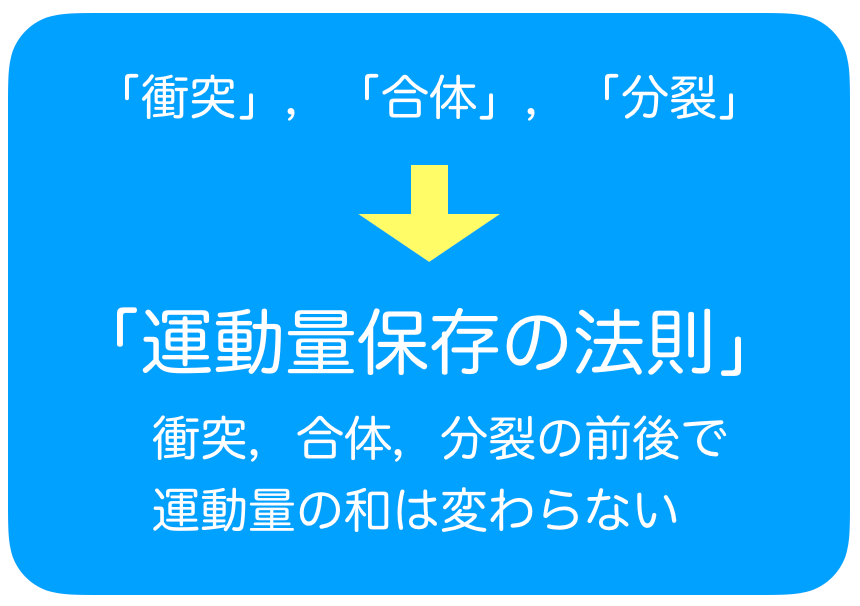
■衝突,合体,分裂→運動量保存則
「衝突」っていうキーワードを見たら,運動量を考えるんだっけ?
「衝突」,「合体」,「分裂」などのキーワードがあったら,運動量を考えて,運動量保存の法則の式を立てるんだね。
運動量保存の法則の式を立てるのね。運動量って
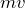
でいいんだっけ?
■運動量は向きを持つ
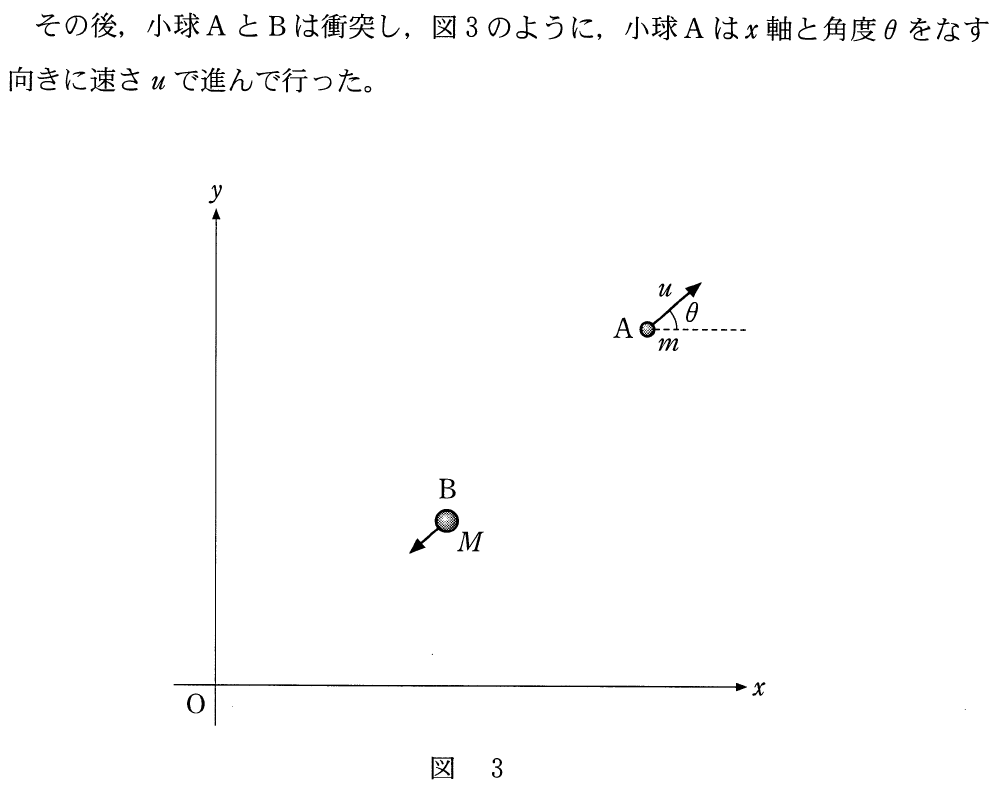
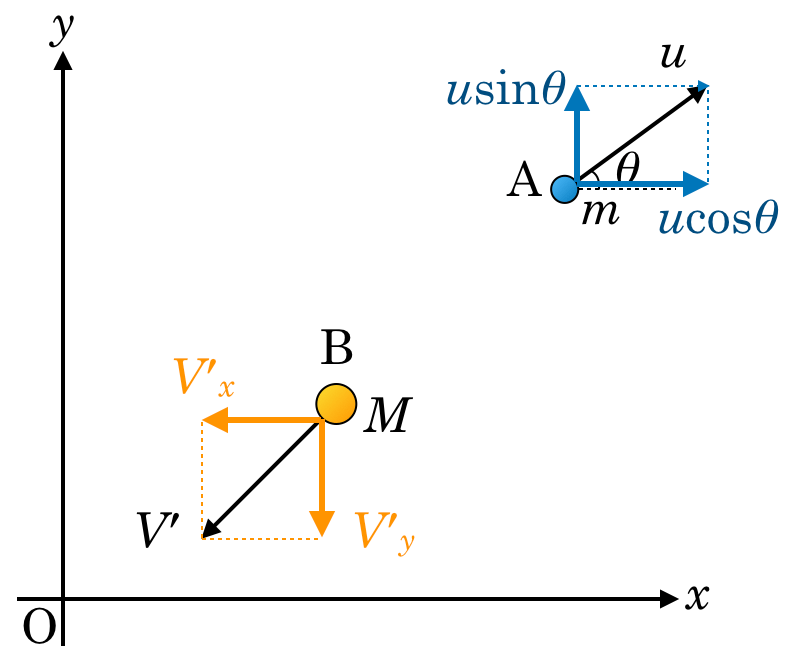
エネルギーと違って,運動量はベクトルなので,向きを考えることも重要なんだ。問題の図の矢印をちょっと長くして描いてみるよ。
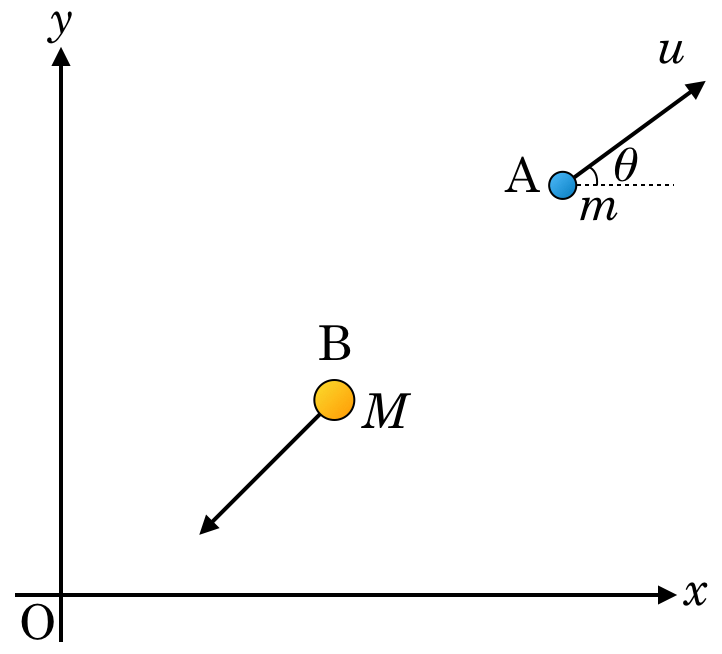
向きを考えるとき,図の小球Aには角度が描いてあるけど,小球Bには描いてないわね。
小球Bの方は正確な向きが分からなくても,速度の
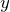
成分の大きさは分かるっていうことじゃないかな。今はその式を求めるんだよね。
それじゃあ,とりあえず2つの小球の速度を

方向と
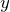
方向に分けるわね。小球Bの速度の大きさが与えられていなかったので,
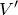
とするわね。
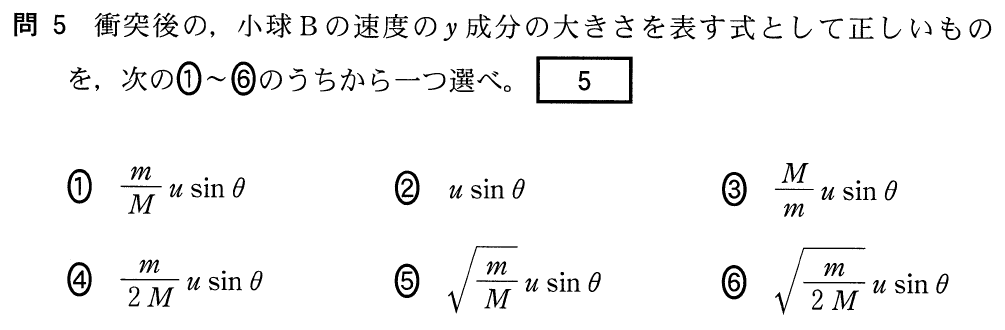
そうすると,今求めたいのは
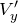
だね。

方向と
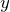
方向に分けて運動量保存の法則の式を立てればいいのね?
そうだね。ただ今求めたいのは
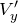
だから,まずは
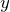
方向だけで,立ててみたら?
それじゃあまず
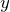
方向だけで,運動量保存の法則の式を立ててみるわ。
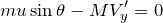
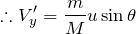
そうなんだよね。

方向の式を立てなくても答えは出るんだ。答えは①だ。



![]() と
と![]() は,
は,![]()
![]()
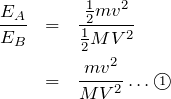
![]() ってやつね。
ってやつね。![]() を消去しようか。
を消去しようか。![]()
![]()
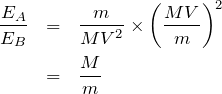



![]() でいいんだっけ?
でいいんだっけ?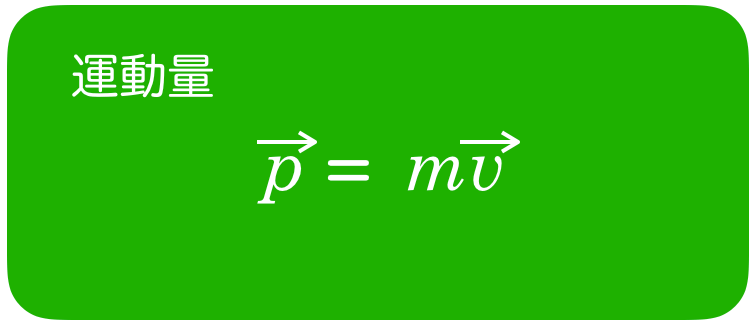

![]() 成分の大きさは分かるっていうことじゃないかな。今はその式を求めるんだよね。
成分の大きさは分かるっていうことじゃないかな。今はその式を求めるんだよね。![]() 方向と
方向と![]() 方向に分けるわね。小球Bの速度の大きさが与えられていなかったので,
方向に分けるわね。小球Bの速度の大きさが与えられていなかったので,![]() とするわね。
とするわね。
![]() だね。
だね。![]() 方向と
方向と![]() 方向に分けて運動量保存の法則の式を立てればいいのね?
方向に分けて運動量保存の法則の式を立てればいいのね?![]() だから,まずは
だから,まずは![]() 方向だけで,立ててみたら?
方向だけで,立ててみたら?![]() 方向だけで,運動量保存の法則の式を立ててみるわ。
方向だけで,運動量保存の法則の式を立ててみるわ。![]()
![]()
![]() 方向の式を立てなくても答えは出るんだ。答えは①だ。
方向の式を立てなくても答えは出るんだ。答えは①だ。