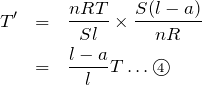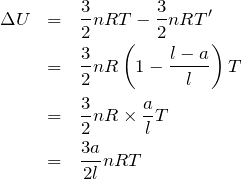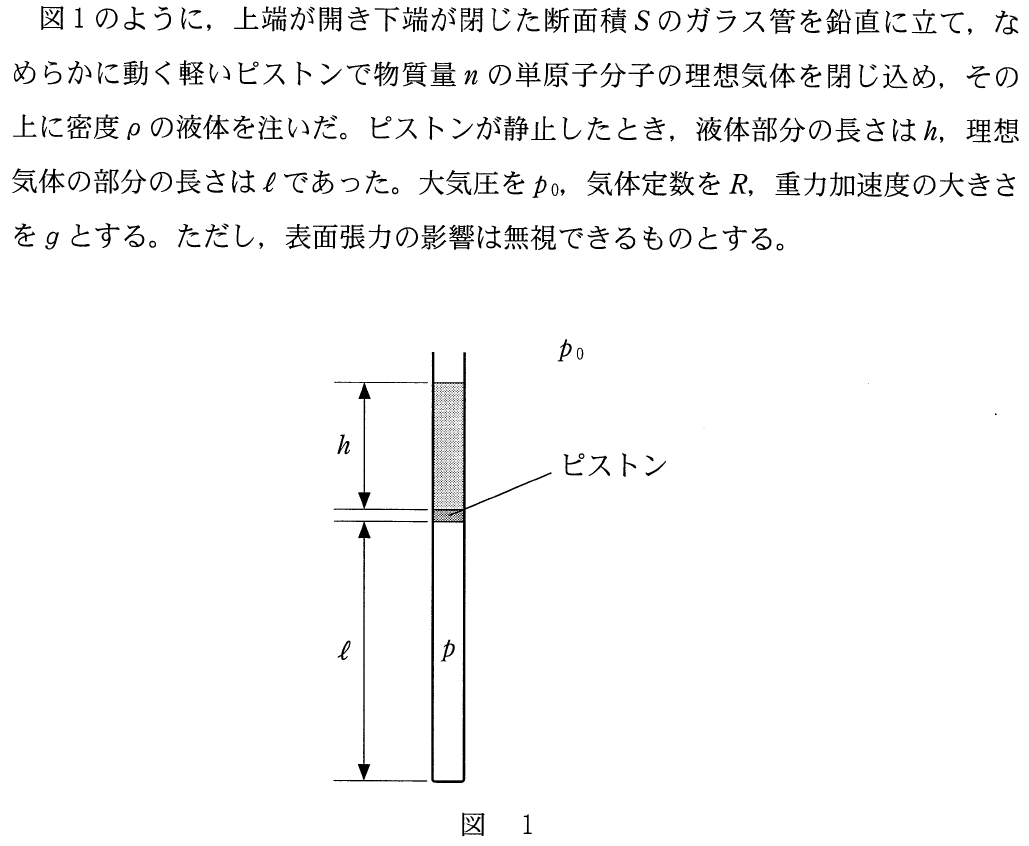
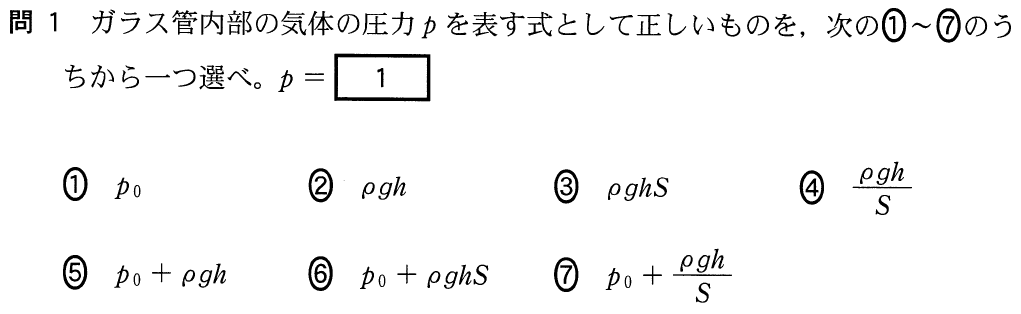
■ピストンにはたらく力の矢印を描く
閉じ込められた気体の問題ね。理想気体の状態方程式とか,ボイル・シャルルの法則を使うと思うんだけど,どう使っていいか分からないわ。
確かに,状態方程式やボイル・シャルルの法則を使う可能性もあるけど,このような問題でまず考えるのはピストンにはたらく力のつり合いだね。
まぁまずはピストンにはたらく力の矢印を描いてみようと思うけど,問題の図に描かれていない情報などもあるので,まずは整理してみるね。
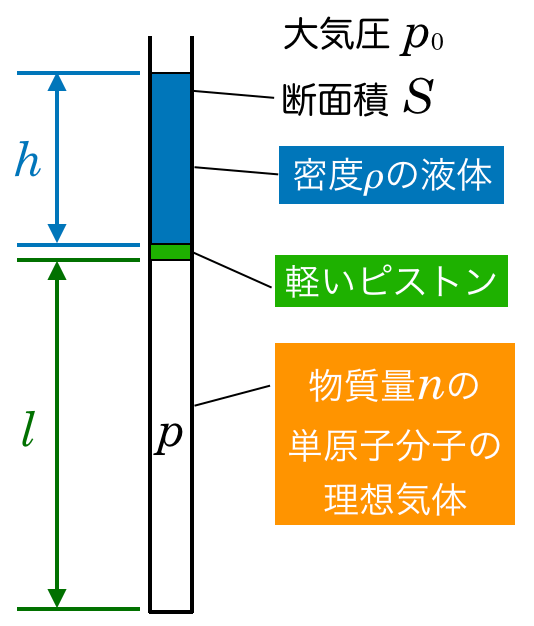
まずはピストンにはたらく重力を考えるんだけど,問題文に「軽いピストン」とあるので,重力は無視できるんだ。
「軽い」っていうのは「重力が無視できる」っていうことね。
次にくっついているものから力を受けるけど,くっついているものは何かな?
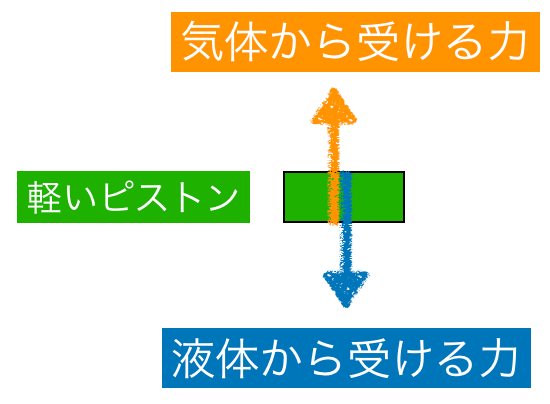
そうだね。ピストンだけ抜き出して描いてみると,こんな感じだね。その力はどのくらいの大きさか分かるかな?
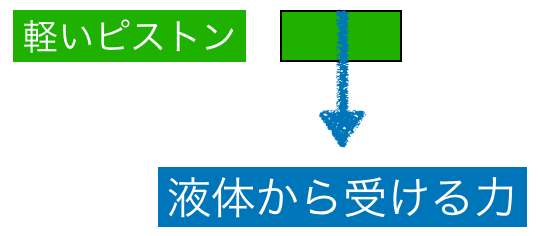
そう考えたくなるけど,違うんだ。ちょっと置いておいて,他にくっついているものはあるかな?
そうだね。周りのガラス管からも力を受けているはずだけど,水平方向の力で,水平方向の力を全て合わせるとつり合っているので,今は考えないことにするよ。ほかにピストンにくっついているものはあるかな?
そう,通常はもう無いと考えるんだけど,これだと液体から受ける下向きの力に対して,上向きの力が無いことになるね。上向きの力がないと,ピストンにはたらく力はつり合わないね。
そうなんだよ。気体が閉じ込められているときは,その閉じ込められている気体から受ける力を考える必要があるんだ。さらに,そのときには,閉じ込められていない気体から受ける力(通常は大気から受ける力)も考えることになるんだ。
■大気から受ける力を描くとき,描かないとき
通常,空気中に物体があるときは大気圧を考えないよね。だけど実際は大気圧による力を受けているんだ。大気圧による力は全方向から受けるので,全てを合わせるとほとんどつり合っているんだ。
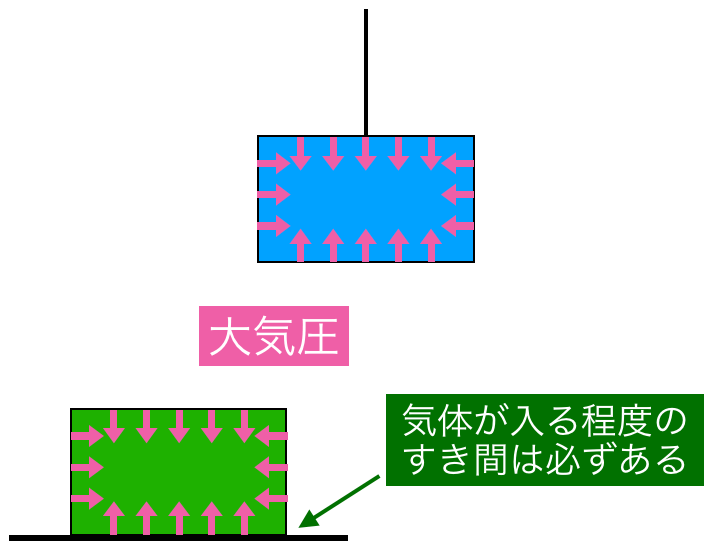
厳密に言うと,大気圧による力を全て合わせると「浮力」になるんだ。この大気中の「浮力」は重力や他の力と比べて,非常に小さいことが多いので無視できるんだね。
熱気球を考えたりするときは,当然浮力は重要な力になるよね。あとは大気中じゃなくて,水中で考えるときには浮力は大切だよ。
話を問題に戻すと,ピストンには上にある液体から受ける力と,下にある気体から受ける力がはたらいていて,つり合っているんだ。気体から受ける力の大きさは分かるかな?
気体の圧力は
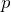
と分かっているのよね。
■圧力
そうだね。でも必要なのは圧力ではなく,力なんだよ。圧力って,この式で求められるよね。

なるほど。ガラス管の断面積は
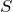
だから,ピストンが受ける力は
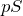
ね。
そうだね。ついでに,液体から受ける力を今は
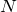
としておこう。
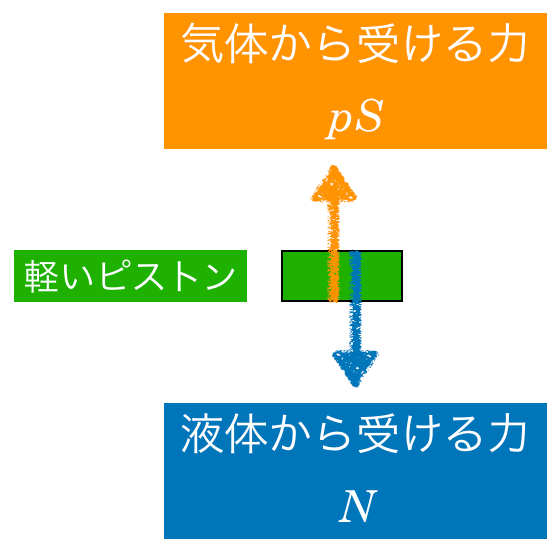
この2つの力がつり合っているのね。鉛直上向きを正として,力のつり合いの式を立てるわね。
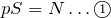
ただ,これだとまだ
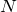
が分からないので,
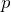
も求められないよね。そこで,今度は液体にはたらく力を考えるよ。
普通はあんまり考えないんだけど,この場合は考える必要があるんだ。
普通の物体と同じように考えていいよ。鉛直方向の力だけ考えようね。
■密度
その代わりに密度が与えられているでしょ。密度って,こういうことでしょ。
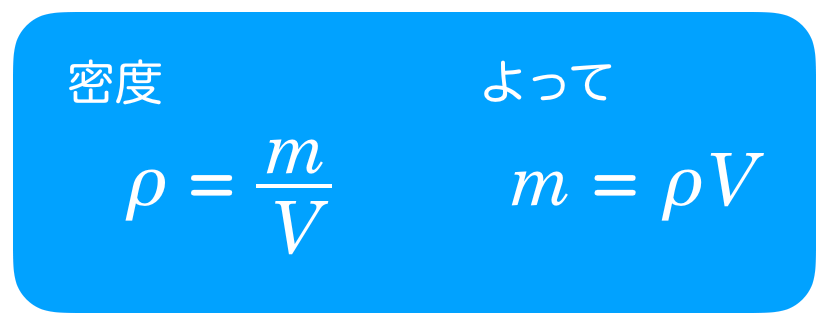
液体の体積は,断面積×高さで
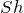
だから,重力の大きさは
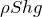
ね。
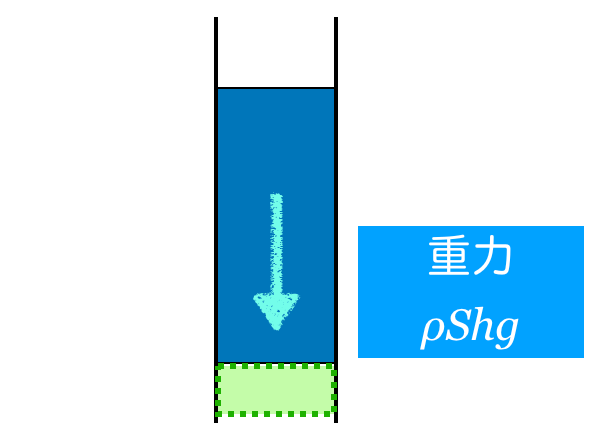
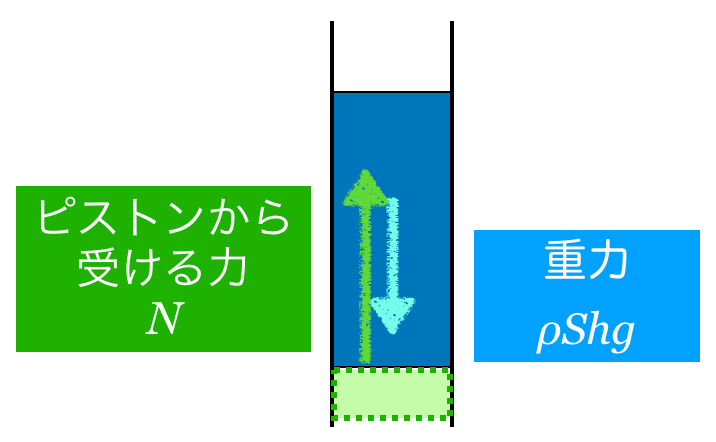
次はくっついているものから受ける力だけど,下にあるピストンから受ける力だね。
さっき,ピストンが液体から受ける力の大きさを
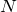
としたので,液体がピストンから受ける力は作用・反作用の関係なので,逆向きに大きさ
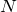
ね。
その通りだ。最後に,大気から受ける力も考えるんだ。この液体とピストンの間には大気が入り込んでいる可能性はないでしょ。
確かに。液体は全方向から大気圧を受けているわけではないっていうことね。
だから下向きの大気圧を考えるんだ。大気圧が
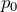
だから,力の大きさは
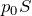
だね。
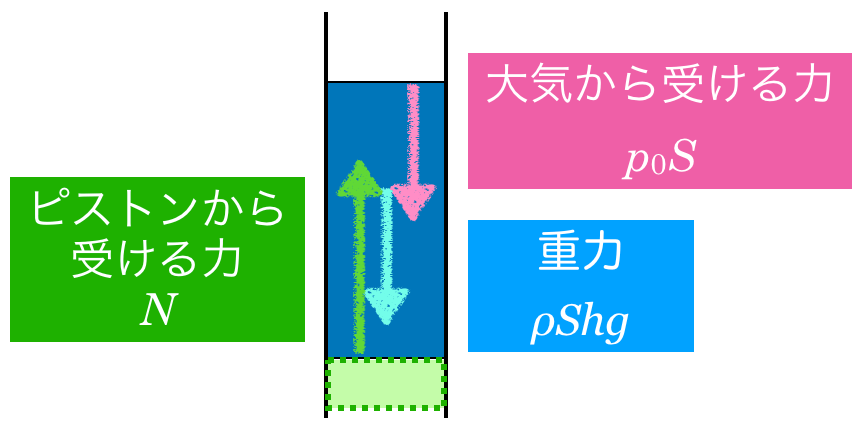
これで全部ね。鉛直上向きを正として,力のつり合いの式を立てるわね。
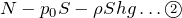
ピストンにはたらく力のつり合いの式①と合わせて
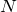
を消去しようか。
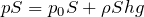
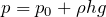
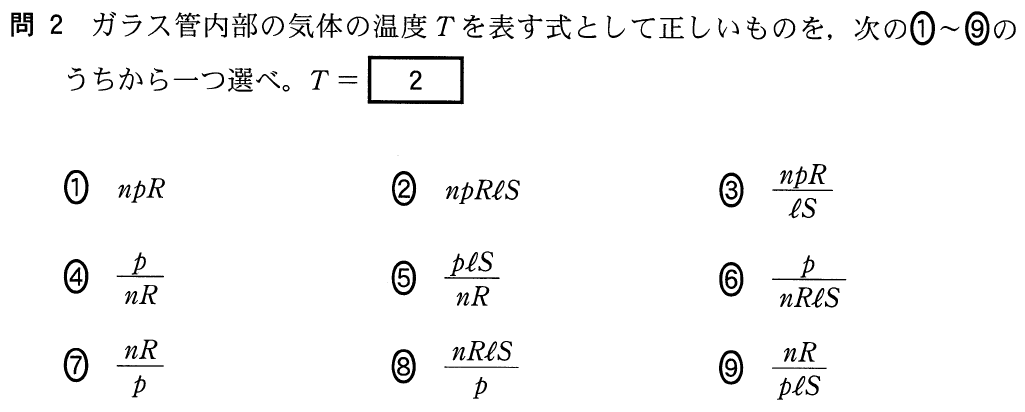
■理想気体の状態方程式
温度を求めるのね。今度こそ理想気体の状態方程式を使うわね。

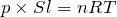
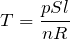
そうだね。これが答えだ。選択肢でいうと⑤だ。最後に問3。
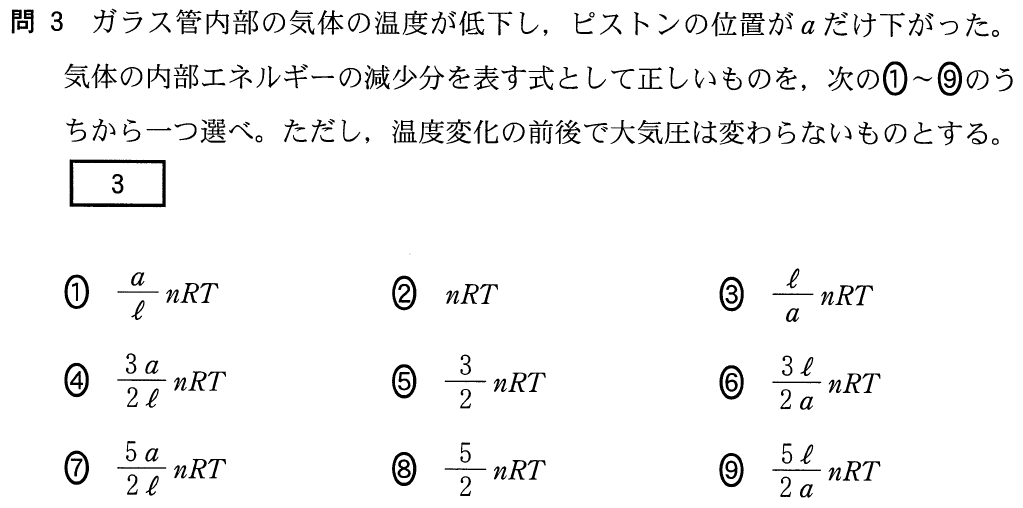
■温度を求める
気体の温度が下がったので,体積が減少して,ピストンの位置が下がったのね。
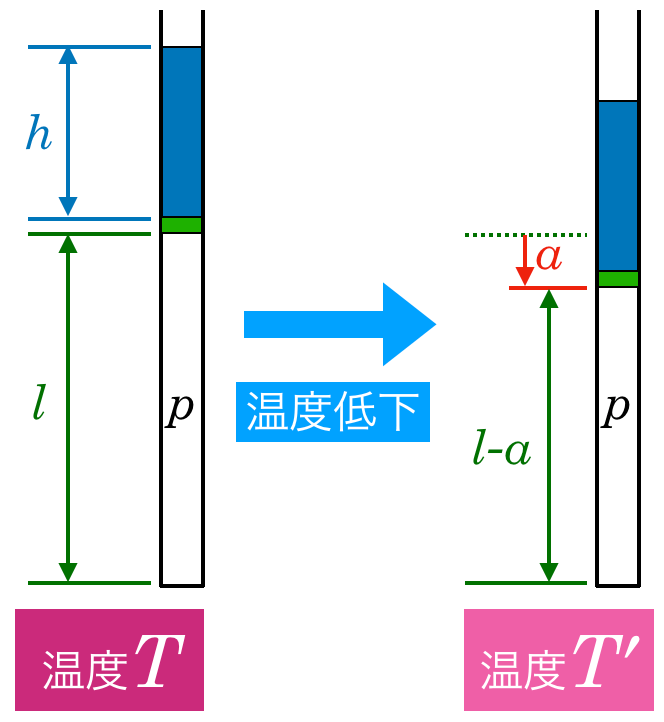
気体部分の高さは

になるのね。温度も下がって
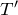
としたのね。気体の圧力は
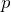
のままでいいの?
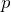
のままでいいんだよ。問1で描いた力の矢印を考えてみると分かるよ。
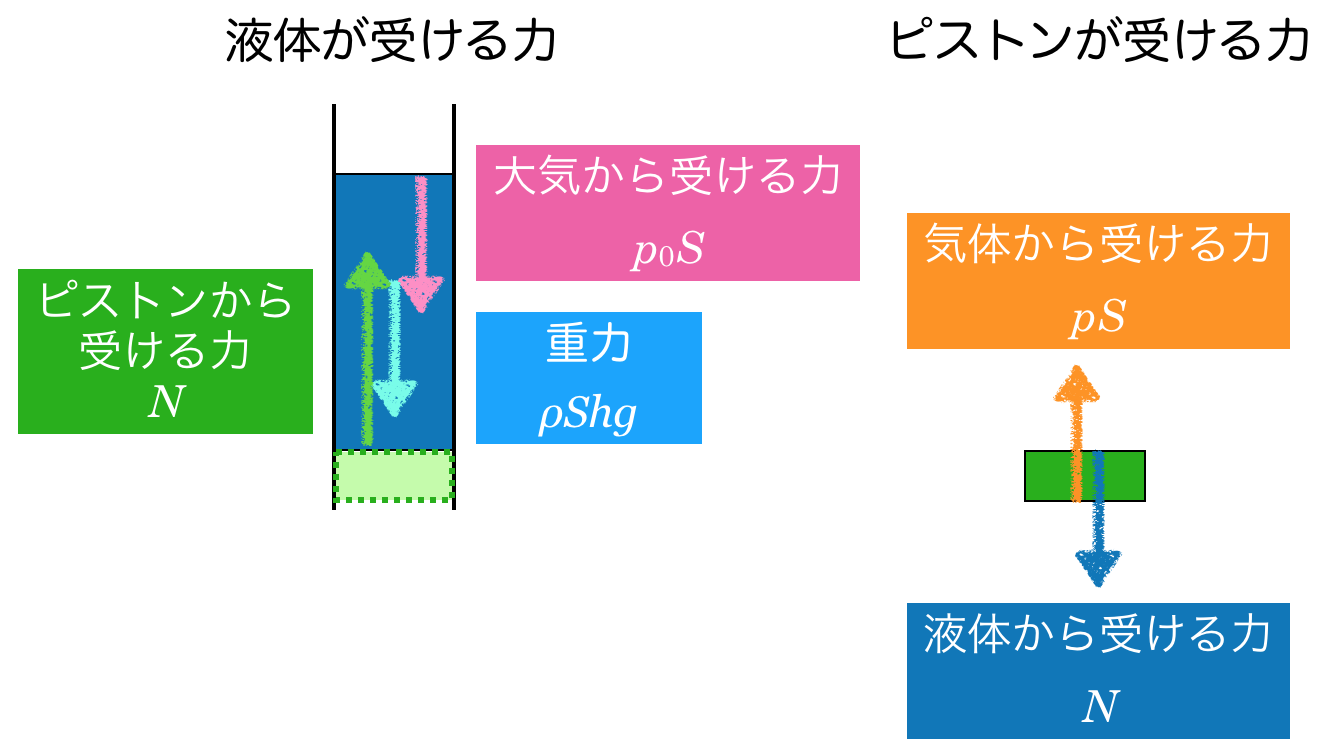
大気圧も,液体の重力も変わっていないよね。ということは,ピストンが液体から受ける力も変わらないから,ピストンにはたらく力がつり合うためには,気体の圧力も変わらないよね。
温度が下がるから圧力も変わりそうだけど,確かにこの場合は変わらないのね。
この段階で一度
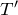
を出しておこうか。
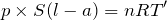
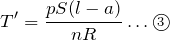
ここで,問2の答えを使って
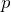
を消去しておこうか。
確かに,選択肢の中には
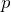
は入っていないもんね。
問2より
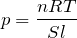
なので,③に代入
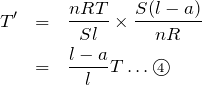
いいね。これはちょっと置いておいて,求めたいのは気体の内部エネルギーの減少分だね。
■内部エネルギーを求める
内部エネルギーって,何となく記憶にあるけど,あんまり覚えてないわ。
よく出てくる言葉ね。「単原子分子」って,ヘリウムとかアルゴンなどの希ガスのことよね。
そうだね。問題文に「単原子分子」っていう言葉があれば,内部エネルギーを思い出して欲しいんだ。

■「変化量」と「減少量」の違い
この式を覚えることにして,結局内部エネルギーは温度に比例するので,温度が分かっていれば,減少分も計算できるということね。
その通り。ただ,「減少分」ってどうやって計算すればいいのか分かる?
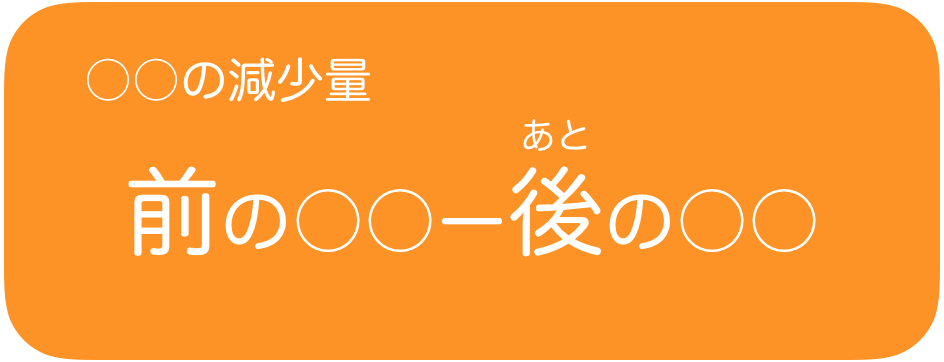
そう,引き算なんだけど,引く順番を間違えちゃダメだよね。分かりにくい「変化量」と「減少量」を比較してみよう。

何でもいいんだけど,例えば「エネルギー」とか「運動量」などだね。
「変化量」を問われたときと,「減少量」を問われたときでは引き算の順序が逆になるのね。
「変化量」は減少しているときは負になってもいいけど,「減少量」を聞かれたときには正で答えなければならないんだね。
今は「減少分」を問われているから,変化前の内部エネルギーから変化後の内部エネルギーを引けばいいのね。
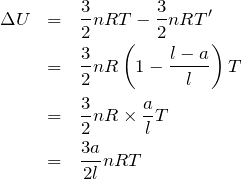






![]() と分かっているのよね。
と分かっているのよね。
![]() だから,ピストンが受ける力は
だから,ピストンが受ける力は![]() ね。
ね。![]() としておこう。
としておこう。
![]()
![]() が分からないので,
が分からないので,![]() も求められないよね。そこで,今度は液体にはたらく力を考えるよ。
も求められないよね。そこで,今度は液体にはたらく力を考えるよ。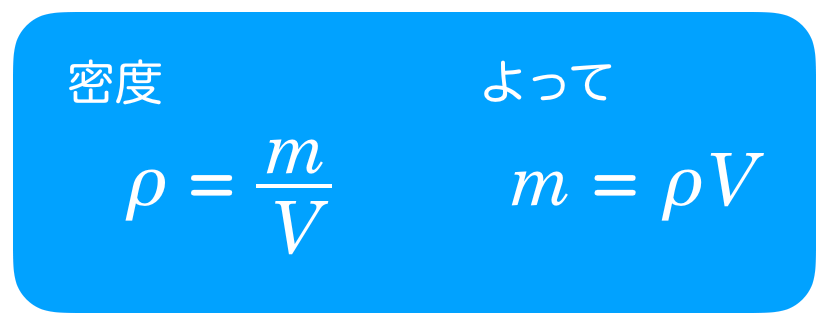
![]() だから,重力の大きさは
だから,重力の大きさは![]() ね。
ね。
![]() としたので,液体がピストンから受ける力は作用・反作用の関係なので,逆向きに大きさ
としたので,液体がピストンから受ける力は作用・反作用の関係なので,逆向きに大きさ![]() ね。
ね。
![]() だから,力の大きさは
だから,力の大きさは![]() だね。
だね。
![]()
![]() を消去しようか。
を消去しようか。![]()
![]()


![]()
![]()


![]() になるのね。温度も下がって
になるのね。温度も下がって![]() としたのね。気体の圧力は
としたのね。気体の圧力は![]() のままでいいの?
のままでいいの?![]() のままでいいんだよ。問1で描いた力の矢印を考えてみると分かるよ。
のままでいいんだよ。問1で描いた力の矢印を考えてみると分かるよ。
![]() を出しておこうか。
を出しておこうか。![]()
![]()
![]() を消去しておこうか。
を消去しておこうか。![]() は入っていないもんね。
は入っていないもんね。![]()