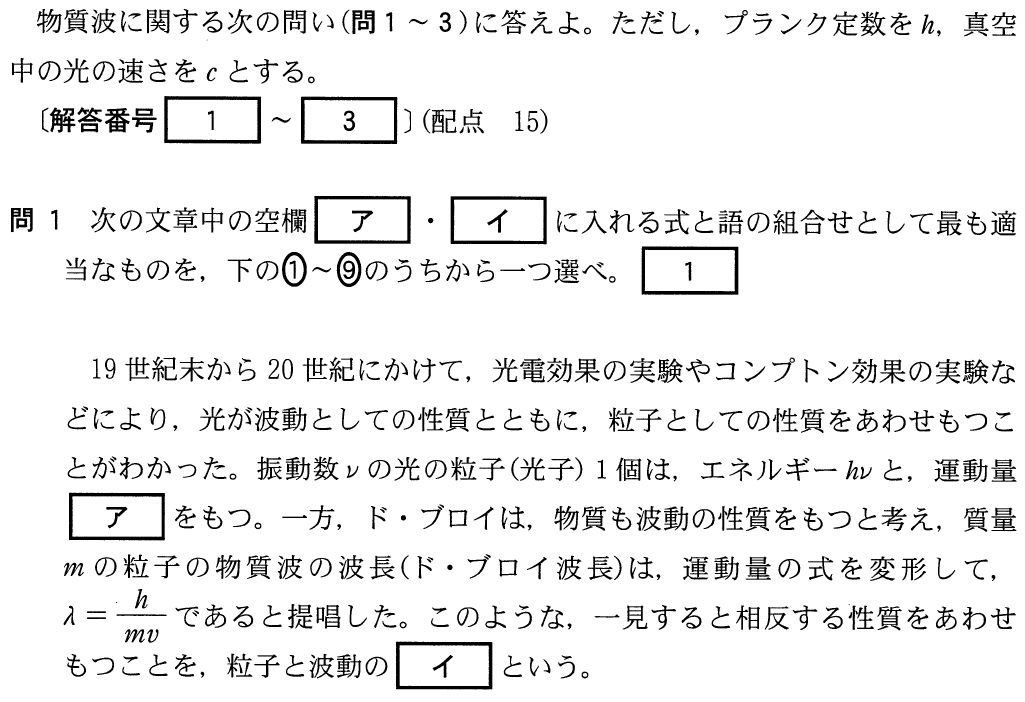
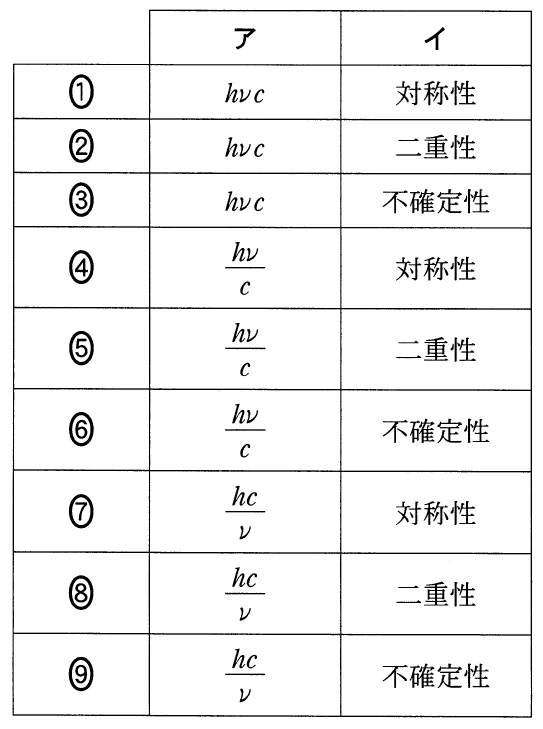
■光子のエネルギーと運動量
「光電効果」や「コンプトン効果」の問題ね。光子のエネルギーや運動量の式は覚えなきゃダメなの?
力学だと,運動エネルギーや運動量の式を覚えているでしょ。それと同じで光子のエネルギーや運動量の式は覚えた方が良いね。この問題ではエネルギーについては問題文にあるけどね。
確かに力学の問題に触れる機会がたくさんあるけど,この原子分野の問題に触れる機会はあまり無いからね。まずは文字の確認をしておこう。

波のところで出てくる
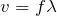
の式が,ここでは
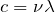
になるのね。
この文字を使うと,光子が持つエネルギーは問題文にある通り,
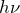
なのね。それで問題は運動量なんだけど,覚えていないわ。
基本的には覚えて欲しいんだけど,「次元」を考えるっていう手があるんだ。
よく空間のことを3次元と言ったり,平面は2次元と言ったりするときの「次元」と同じなんだけど,長さだけじゃなくて,他の物理量についても次元を考えることができるんだ。
そんな感じかな。詳しいことは調べてみて。今考えたいのは,力学で出てくる運動エネルギーって,係数であるの2分の1を除くと,「質量×速さ2」で計算できるでしょ。

だからね。
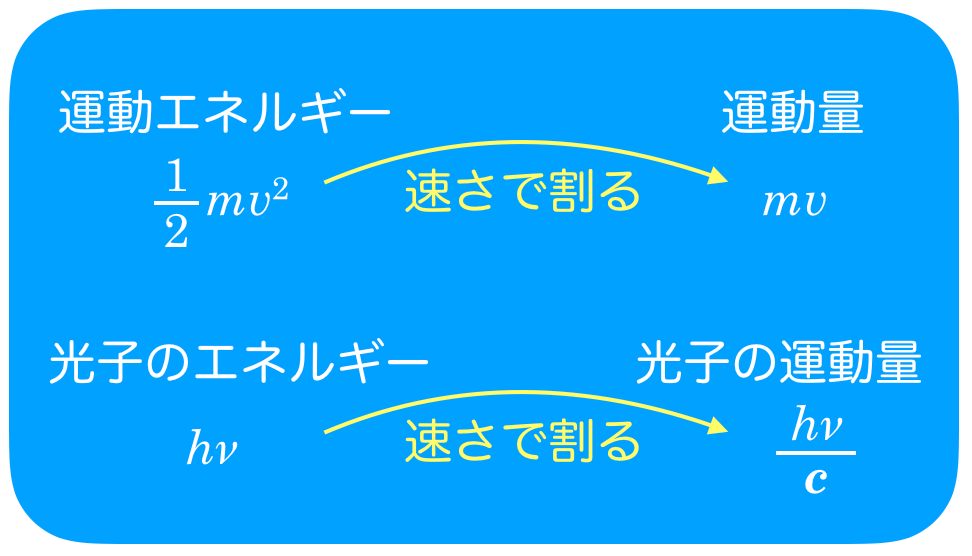
この運動エネルギーを「速さ」で割ると,運動量「質量×速さ」になるでしょ。
この関係が,光子のエネルギーと運動量の間にも成り立つんだ。光子の場合の速さは

ね。
■「粒子性」と「波動性」
④〜⑥のどれかね。もう一つの空欄は「粒子と波動の」対称性か,二重性か,不確定性ね。どれも入りそうな気がするわ。
「一見すると相反する性質をあわせもつことを,粒子と波動の」に続く言葉なのよね。「相反する」というのは,「波動としての性質」と「粒子としての性質」の2つね。この2つをあわせもつんだから,空欄に入るのは「二重性」かな?
その通りだよ。2つの性質を持っているから「二重性」だ。この言葉も覚えていた方が良いね。答えは⑤だ。

■平均運動エネルギーと温度
しかも,分子の平均運動エネルギーと温度の話という,ちょっと難しい話だね。この話は,気体の分子運動論の後半に出てくるんだよ。覚えているかな?
覚えていないけど,問題文に「分子の平均運動エネルギーは温度だけで決まる」と書いてあるからこの関係を使えばいいわよね。
そうなんだけど,どんな関係かが書かれていないよね。比例関係とか,二乗に比例するとか。
まぁこれは覚えているしかないんだけど,こんな関係なんだ。

ということは,分子の平均運動エネルギーと,温度は比例関係ね。
■温度とド・ブロイ波長
そういうことだね。今は温度が

から4

と4倍になるので,分子の平均運動エネルギーはどうなるかな?
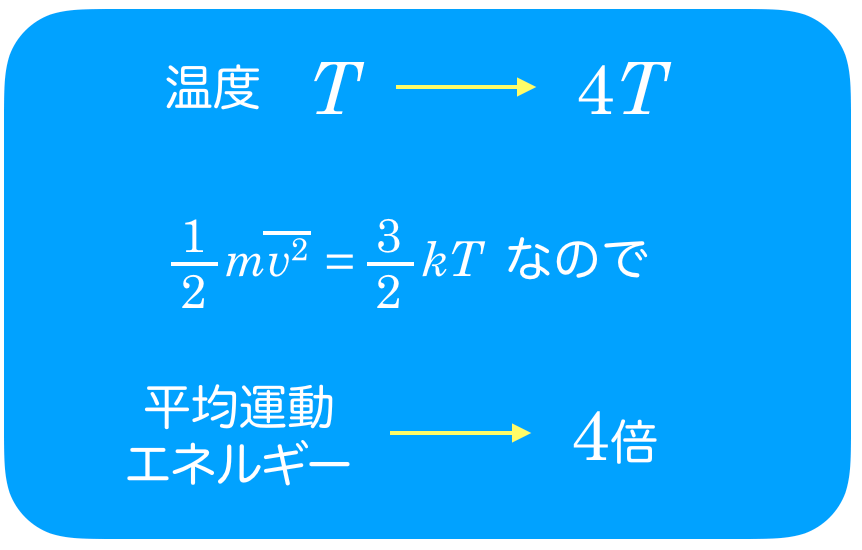
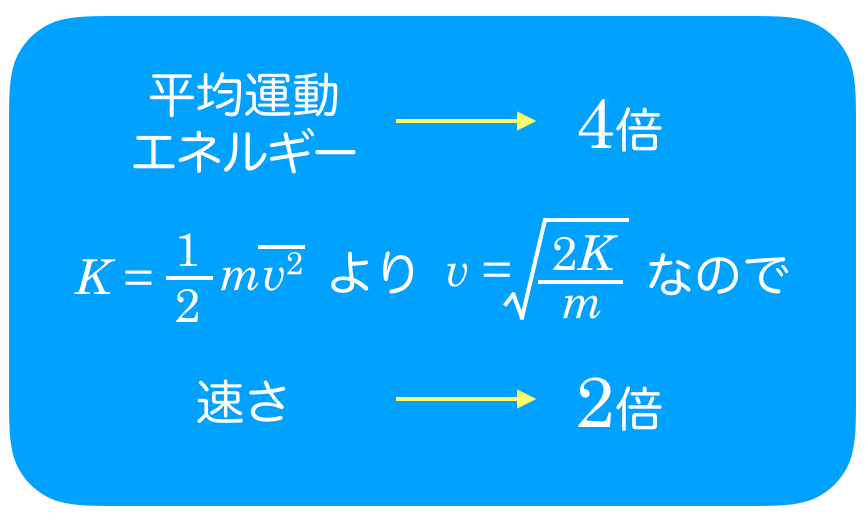
次は,分子の平均運動エネルギーが4倍になると,速さは何倍になるかな?
運動エネルギー
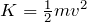
が4倍になるんだから,速さは2倍ね。
そうだね。そうすると,ド・ブロイ波長はどうなるかな?
ド・ブロイ波長は問1の問題文にあったわね。
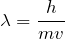
なので,速さが2倍になると,波長は2分の1倍ね。

■波動性を示す証拠
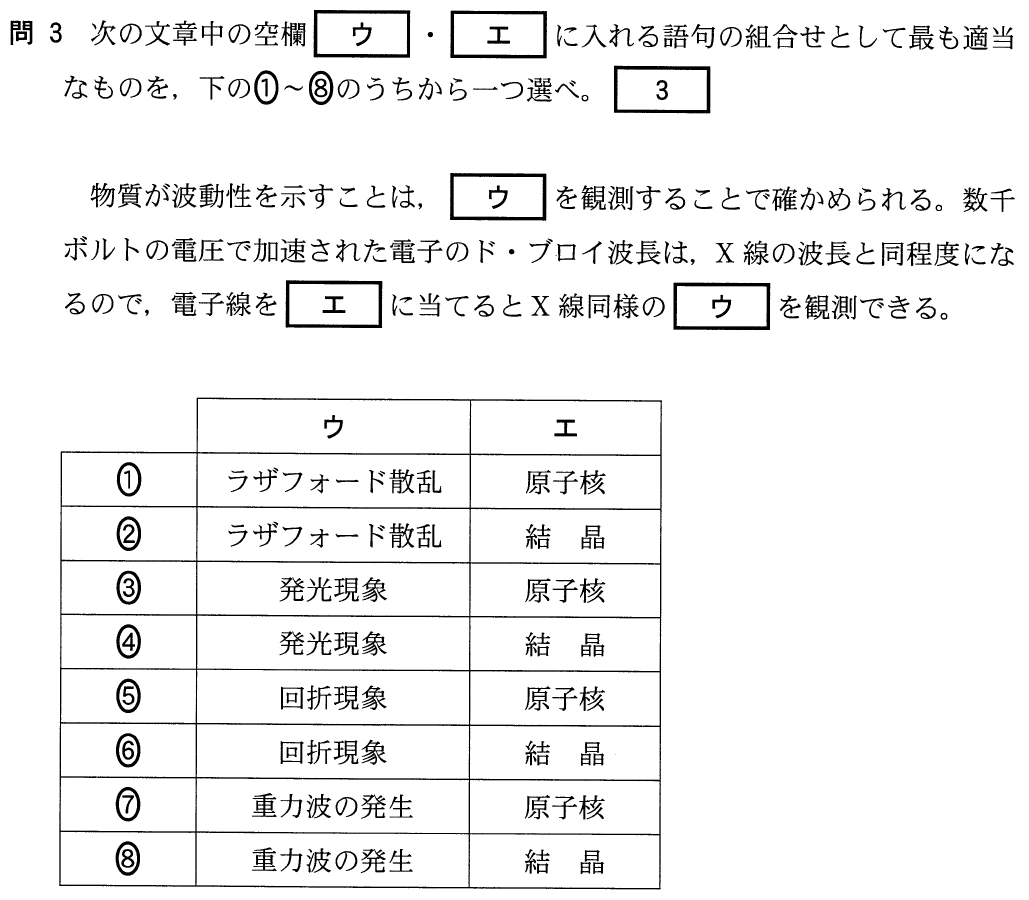
最初の空欄は物質が波動性を示す証拠だから,波動特有の現象が入るわよね。
間接的に波動性が分かる可能性もあるけど,それは難しいよね。最後の空欄も同じ言葉が入るので,X線も起こす現象だね。
選択肢の「ラザフォード散乱」はラザフォードが付いているけど,「散乱」って波動現象よね。
確かに空が青く見えるのは光の散乱によるものだね。ただ「散乱」は波動特有の現象ではないね。高校の物理の教科書に出てくる「ラザフォード散乱」はヘリウムの原子核であるアルファ粒子が金の原子核とぶつかって進行方向が変わる,つまり散乱する現象のことを言うね。
それじゃあ,ラザフォード散乱が起こることで,波動性は証明できないのね。
そういうことだね。その次にある「発光現象」も,光は波動だけど,「光ること」については波動性は関係ないね。
これが波動性を示す証拠だね。防波堤で海の波が回折するとか,塀で音が回折するとか,細いスリットで光が回折するとか,波動特有の現象だね。
それじゃあ,答えは⑤か⑥ね。最後の選択肢にある「重力波の発生」は?
これも重力波自体は波動現象だけど,重力波を発生するのには,波動現象は関係ないよね。
最後は「ウ」の空欄に入れてみると,「電子線を( エ )に当てるとX線同様の回折現象を観測できる。」となるわね。「原子核」に当てるか,「結晶」に当てるかね。
X線を「原子核」に当てるとか,「結晶」に当てるなどの実験を聞いたことがある?
そういえば,聞いたことがあるわ。「X線回折」っていうやつね。
そう。それってX線を「原子核」に当てる?「結晶」に当てる?
確かX線回折って,結晶構造を調べるのに使われるんじゃなかったっけ?
その通りだよ。なので,答えは「結晶」に当てるという,⑥だね。



![]() の式が,ここでは
の式が,ここでは![]() になるのね。
になるのね。![]() なのね。それで問題は運動量なんだけど,覚えていないわ。
なのね。それで問題は運動量なんだけど,覚えていないわ。![]() だからね。
だからね。![]() ね。
ね。


![]() から4
から4![]() と4倍になるので,分子の平均運動エネルギーはどうなるかな?
と4倍になるので,分子の平均運動エネルギーはどうなるかな?
![]() が4倍になるんだから,速さは2倍ね。
が4倍になるんだから,速さは2倍ね。
![]()


 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!


![]() の式が,ここでは
の式が,ここでは![]() になるのね。
になるのね。![]() なのね。それで問題は運動量なんだけど,覚えていないわ。
なのね。それで問題は運動量なんだけど,覚えていないわ。![]() だからね。
だからね。![]() ね。
ね。


![]() から4
から4![]() と4倍になるので,分子の平均運動エネルギーはどうなるかな?
と4倍になるので,分子の平均運動エネルギーはどうなるかな?
![]() が4倍になるんだから,速さは2倍ね。
が4倍になるんだから,速さは2倍ね。
![]()

