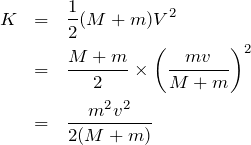
■運動エネルギーを求めたい
パックマンみたいだね。左からくる小物体を食べちゃうしね。
問題作成者にとってはあるんだろうけど,解く側の立場ではあまり気にしなくていいんじゃないかな。
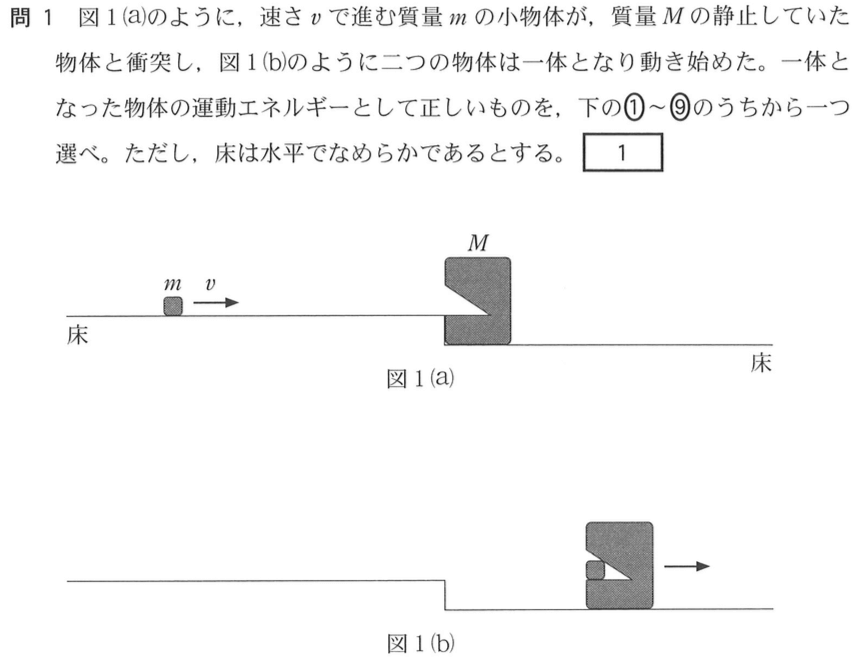
それじゃあまず問題文を確認すると,運動エネルギーを求める問題ね。
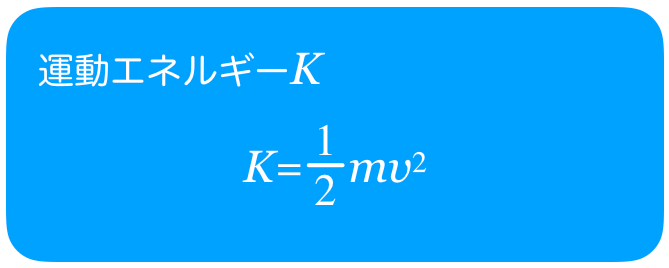
そうだね。今求めたいのは「一体となった物体の運動エネルギー」だから,一体となったときの質量と速さがわかればいいね。
一体となったときの質量は
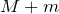
よね。速さは?
もしかして,「力学的エネルギー保存則」で求めるんじゃない?
残念ながら力学的エネルギーは保存されないんだ。衝突のときに減るんだよ。
物体の運動によって速さの求め方はいろいろあるけど,この問題の場合は問題文中にキーワードがあるよ。
キーワード?「床は水平でなめらか」っていうところ?
それも大切なことではあるね。「床は水平」っていうのは「斜面じゃないから加速しないよ」っていう意味で,「なめらか」っていうのは・・・
そうだね。もっと重要なキーワードがあるんだ。「衝突」だよ。
■「衝突」「合体」「分裂」で運動量保存の法則
問題文に「衝突」というキーワードがあると「運動量保存の法則」を使う可能性が高いんだ。
運動量って
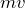
だっけ?

2つの物体が「衝突」したり,「合体」したり,1つの物体が「分裂」したりする前と後で運動量の和が保存されるんだ。
運動量を考えるので,図の中に質量と速度を書き込もう。
それじゃあ,一体となった後の速度を

とするね。
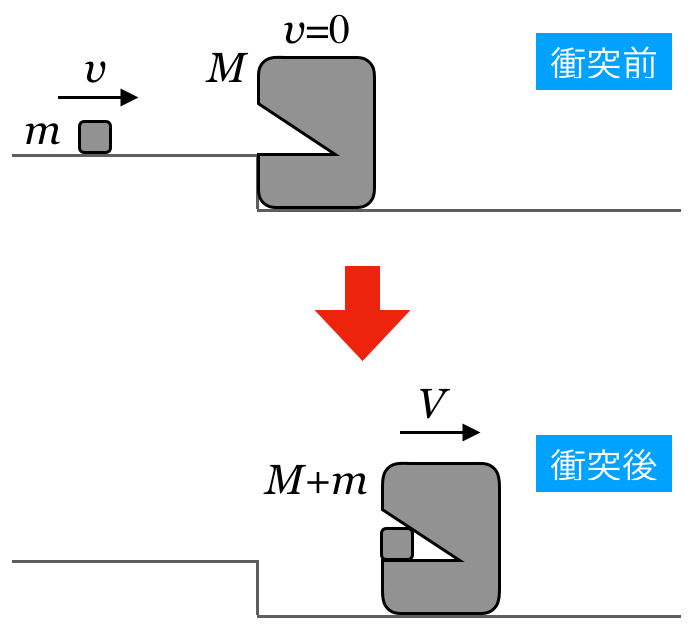
いいね。それでは,この図を見ながらこんな式を立てるんだ。

その通りだよ。運動量はベクトルだから,向きも考慮しなきゃダメだね。
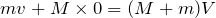
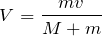
求めたいのは「一体となった物体の運動エネルギー」だ。
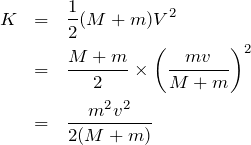

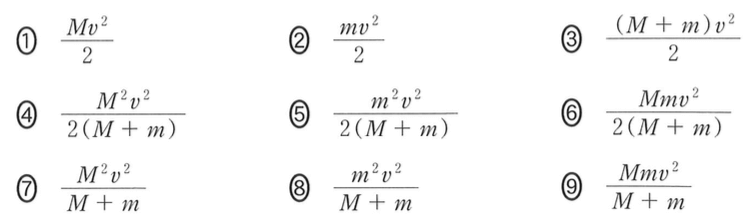
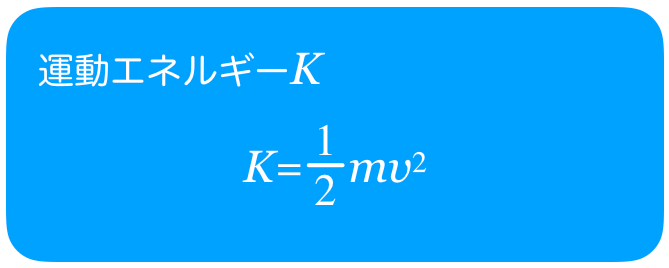
![]() よね。速さは?
よね。速さは?![]() だっけ?
だっけ?
![]() とするね。
とするね。

![]()
![]()
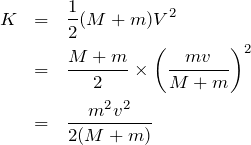
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!
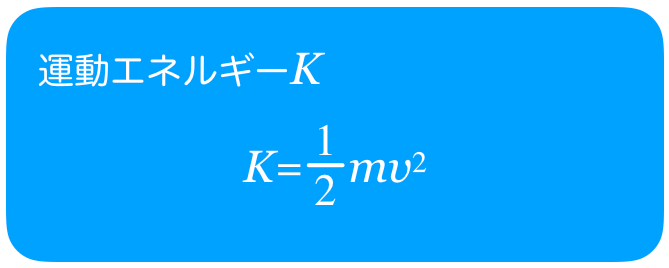
![]() よね。速さは?
よね。速さは?![]() だっけ?
だっけ?
![]() とするね。
とするね。

![]()
![]()