■ファラデーの電磁誘導の法則
グラフを選ぶ問題ね。電池も何もないけど,コイルに電流は流れるの?
あー電磁誘導か。ファラデーの電磁誘導の法則っていうやつ?

まぁ確かに最初からマイナスがついていたり,あまり見かけない
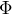
という文字が入っていたり,いやな感じではあるよね。一応この式を使っても答えは出せるんだけど,この式から導き出される次の式の方が使いやすいんだ。

棒に生じる起電力が関係しているときには,この式が便利なんだ。今は,コイルの辺abが磁場(磁界)に入るまでは,起電力は生じないからコイルに流れる電流は0ね。
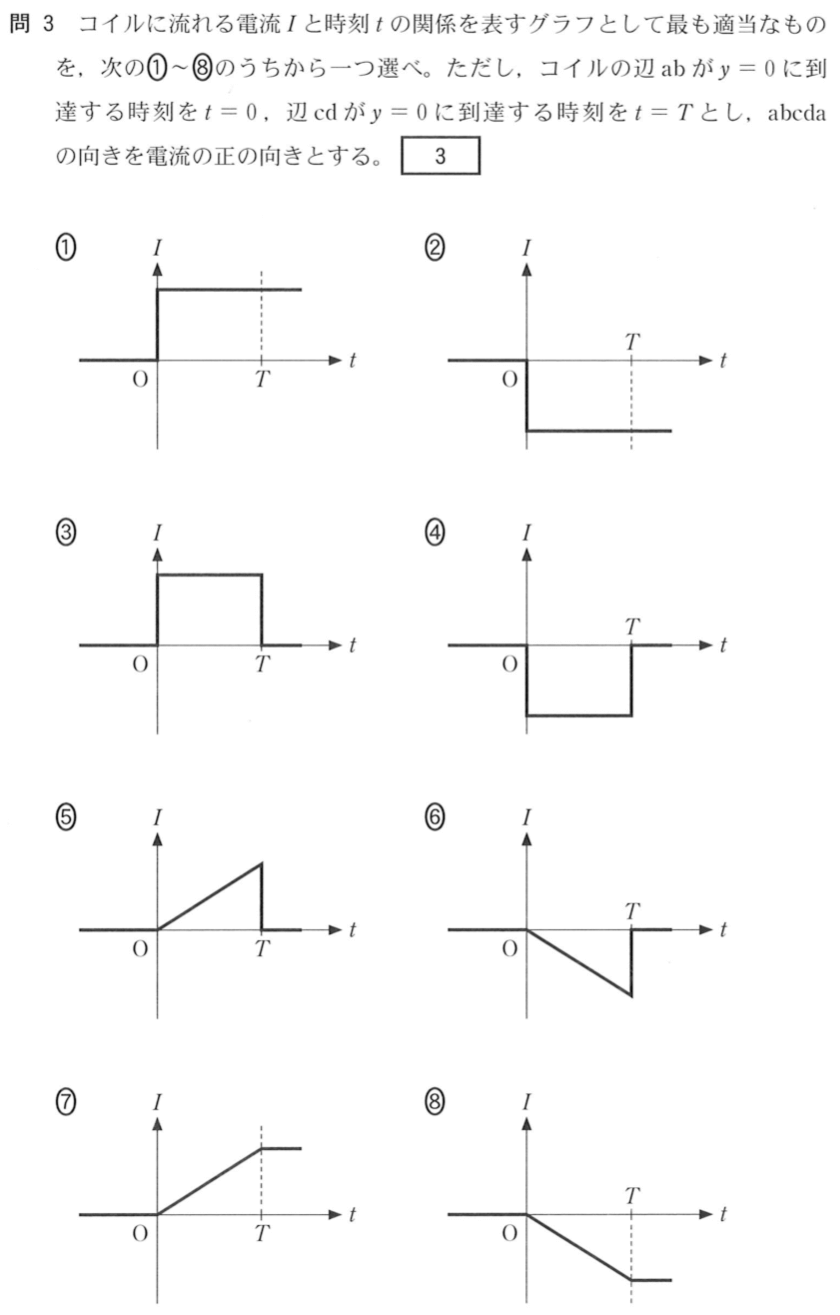
確かにどのグラフも原点より左側は0になってるわね。
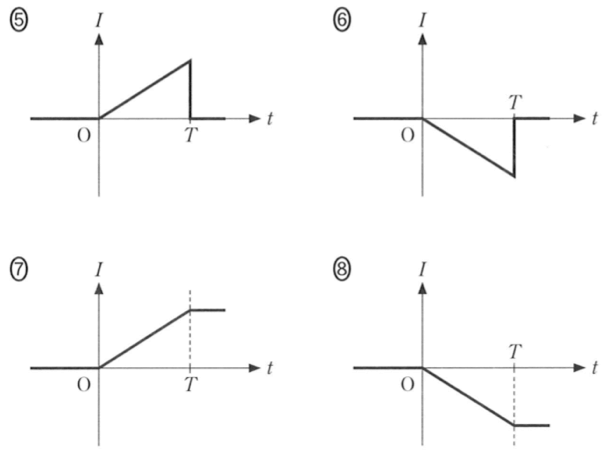
原点より右側は,①から④のように急に電流が流れるか,⑤から⑧のように徐々に電流が大きくなるのかは,分かるかな?
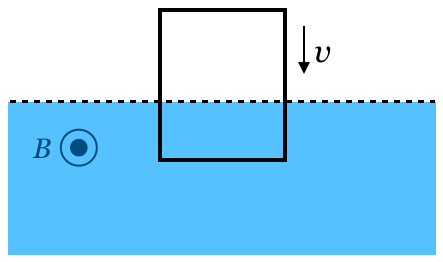
そこは大切だね。次の問4では,その一定の速さ

を求めることになっているよ。
速さを

とすると,さっきの式
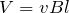
が使えるのね。
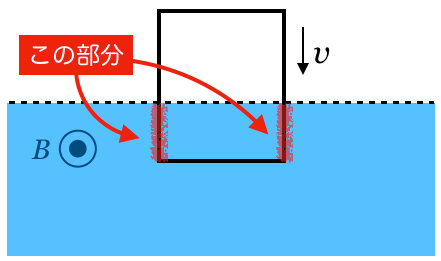
磁場に垂直な辺だけを考えるんだよ。磁場の向きに磁力線があるんだけど,その磁力線を横切っている部分だけを考えるんだ。だから,横の辺は考えなくていいんだね。
なるほど。ということは,辺abだけを考えればよくて,発生する起電力

は,
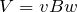
となるわね。
そうだね。そうすると,コイル全体の抵抗が
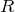
だから,流れる電流
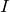
はどうなるかな?
オームの法則でいいわよね。
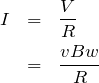
そうだね。ということは,電流は時間によらず一定値ということだよね。つまり,⑤から⑧のグラフではないということだ。
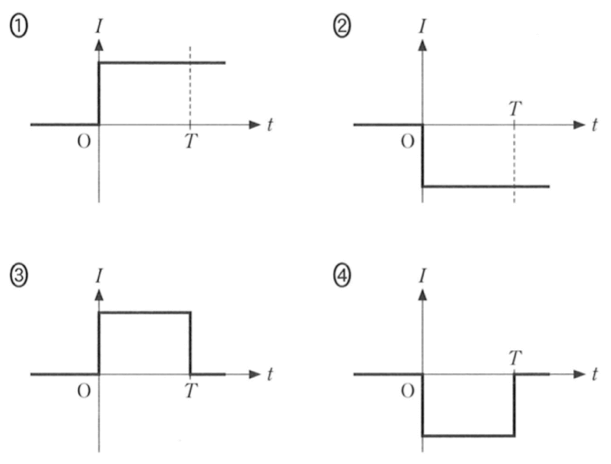
次は,流れる電流の向きが正か負かね。電流の向きはどうやって求めるの?
さっきのファラデーの電磁誘導の法則の,「コイルの磁束の変化をさまたげる向きに起電力が生じる」ということから求めてもいいし,コイルの中の自由電子が受けるローレンツ力の向きから求めることができるよ。
磁場中で荷電粒子が運動している時に受ける力のことだけど,これはまぁ別の所で話をすることにして,もう一つ電流の向きを求める方法があるんだ。
■フレミング”右手”の法則
そう右手。左手の法則と同じように,右手の中指,人差し指,親指がそれぞれ直角になるようにするんだ。
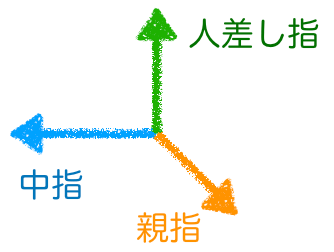
そうすると,誘導起電力,磁場,運動の向きを示してるんだ。
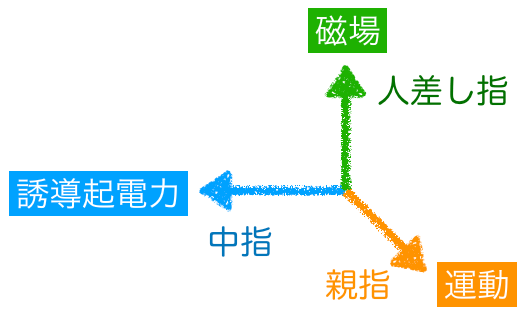
一般的には,中指から順に「電磁動」と覚えるといいよ。
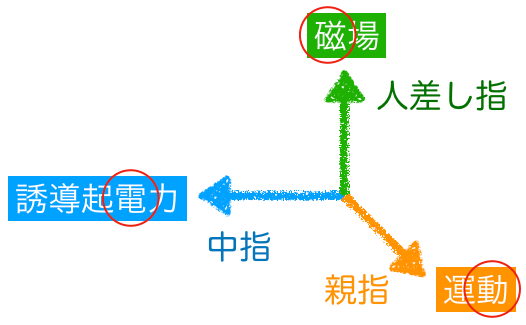
それじゃあ,フレミング右手の法則を使ってみると,人差し指が磁場の向きだから,紙面に垂直で裏から表の向きね。親指は運動の向きだから下向きよね。
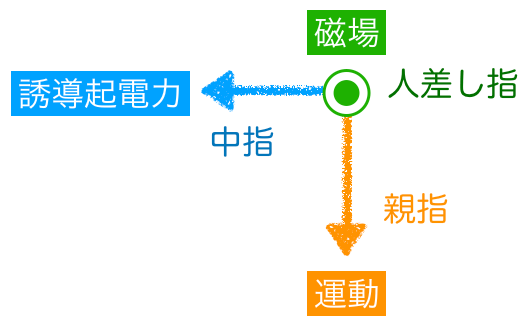
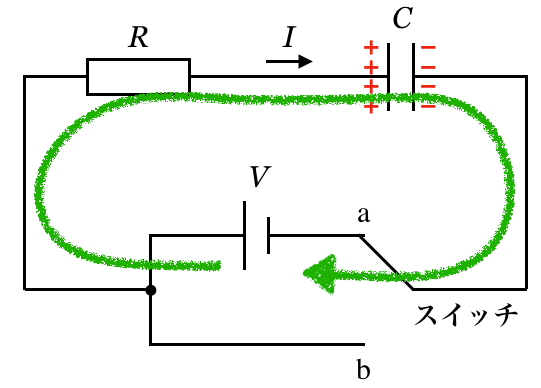
誘導起電力の向きが左ということは,回路に書き込むとこんな感じになるということだよ。
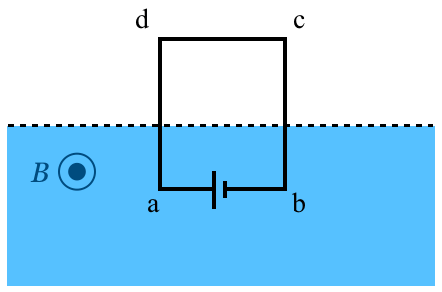
a側が正極の電池ということね。ということは,電流はadcbaの向きに流れると考えていいわよね。
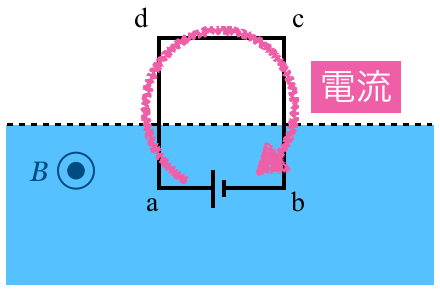
abcdaの向きが正だから,電流は負だね。これで,②か④に絞られたね。
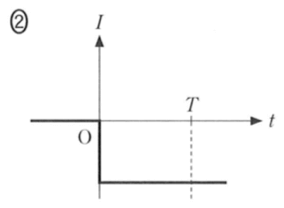
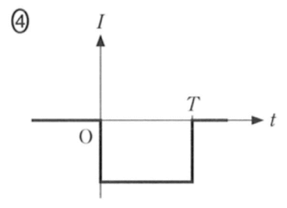
あとは,時刻

で電流が0になるのか,そのまま電流が流れ続けるのか,という2択ね。
時刻

はコイルがすべて磁場に入った時だよね。
コイルが全部磁場に入っても,辺abに生じる誘導起電力はそのままよね。磁場中を導体棒が運動すれば誘導起電力が発生するんだから。
確かにその通りだ。その通りなんだけど,コイルが全部磁場に入ると,今度は辺dcにも誘導起電力が生じるんだ。
そうか。辺dcも磁場の中で下向きに動いているから,辺abと同じように誘導起電力が生じるのね。
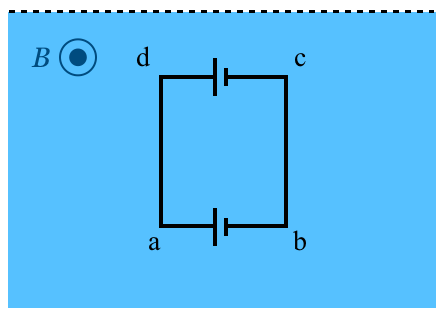
そうだね。辺abにも辺dcにも左向きの誘導起電力が生じるから,打ち消し合って結局電流は流れないんだ。
どちらの誘導起電力も,大きさが
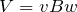
だから,逆向きで打ち消し合うということね。
そういうことだね。別の考え方として,コイルがすべて磁場に入ると「コイルを貫く磁束が変化しないので誘導起電力は生じない」,としてもいいね。
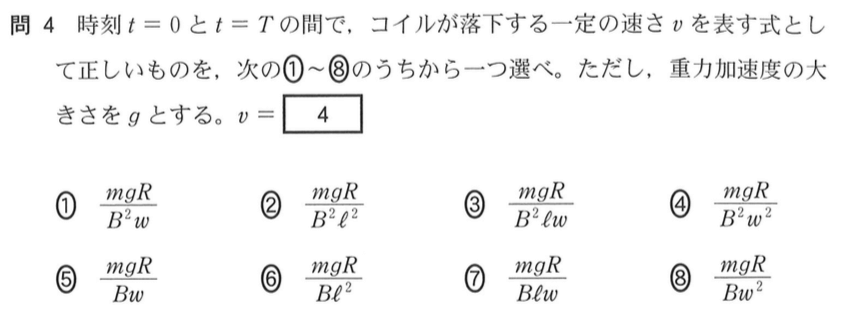
■「等速」なら「力のつり合い」を考える
「一定の速さ

」を求める問題ね。等速だから,速さ=距離÷時間よね。つまり,
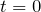
から
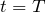
の間に
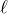
だけ落下するから,こうね。
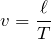
その通りだよ。そうなんだけど,選択肢の中にその答えがないよね。
ということは,
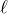
か

を他の文字で表せばいいわよね。
他の方法を考えるしか無いんだよ。これがセンター試験などのマーク形式の問題のイヤなところだね。選択肢がある問題は選べばいいだけだから簡単な感じもするけど,自分の出した答えが合っているのに選択肢に無い,ということもあるんだよ。

そういう時は,別の方法を考えるしか無いのね。等速だから,速さ=距離÷時間を使うと思ったけど,使わないとすればどうすればいいの?
「一定の速さ」というキーワードで思い出して欲しいのは,「力のつり合い」なんだ。

そうか,力がつり合っていれば等速直線運動をするんだから,逆に等速直線運動をしていれば,力がつり合っていると考えていいのね。
必要なのは,コイルが途中まで磁場に入っているときの図ね。それじゃあ,まずは重力ね。
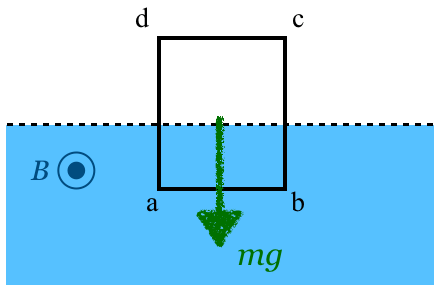
あとは,くっついているものがないので,これで終わり?
そうよね。鉛直上向きの力がはたらいているはずよね。
鉛直上向きにはたらいているのは,電流が磁場から受ける力だね。
あっそうか,「フレミング左手の法則」で求める力ね。
そうだよ。ただフレミング左手の法則では,力の向きしか分からないけどね。
そうか,力の向きは,鉛直上向きって決まっているのよね。
その通り。力の向きはすでに分かっているんだ。でも一応確認しておこうか。電流の向きはこうだったね。
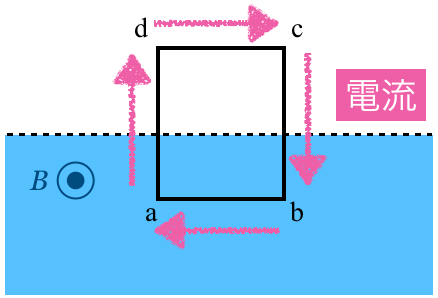
ということは,フレミング左手の法則より,電流が磁場から受ける力はこうね。
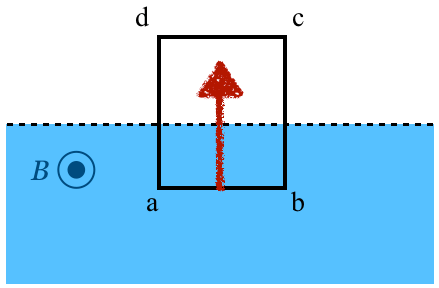
確かにコイルの辺abが受ける力は鉛直上向きだけど,左右の辺も力を受けるよ。
あっそうか忘れてた!左右の辺にも力がはたらくのね。こんな感じ?
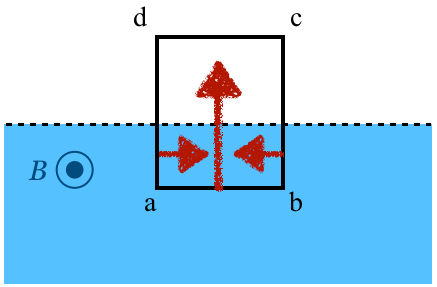
そうだね。この左右方向の力は逆向きで同じ大きさの力だから,つり合っていて今は考えなくていいね。
長さ
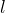
の導線を流れる電流
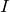
が磁束密度Bの磁場から受ける力の大きさ
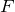
は,こう表せるんだ。

フレミング左手の法則からもわかるけど,この式の
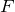
,
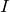
,
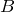
はそれぞれ垂直の関係だからね。垂直じゃない場合は,垂直な成分を考えることになるよ。
フレミング左手の法則を考えるときの指も,それぞれ垂直な方を指すものね。
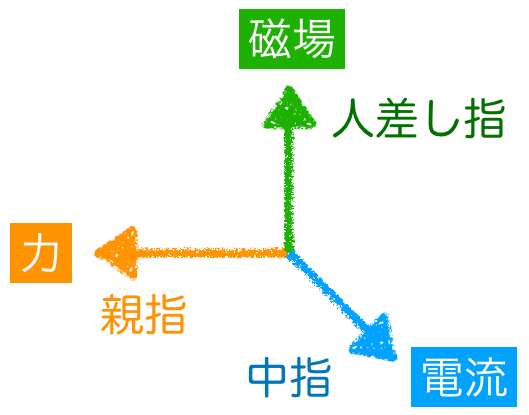
そういうことだね。コイルにはたらく左右方向の力を見てみると,左右の辺で,
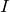
,
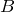
,
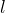
がすべて同じだから,はたらく力の大きさ
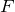
も同じなので,力がつり合っているんだね。
それじゃあ,あらためてコイルにはたらく力を考えてみると,辺abの長さが
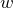
だからこんな感じね。
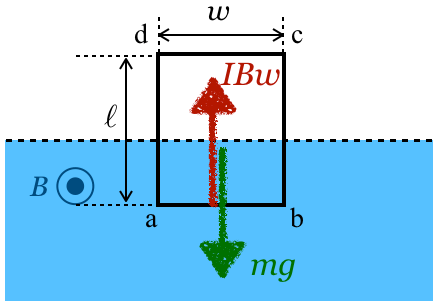
そして,コイルが一定の速さで落下しているから,鉛直方向の力もつり合っているんだよね。
求めたいのはその一定の速さ

だけど,鉛直方向の力のつり合いの式を立てても

は出てきそうもないわ。一応鉛直上向きを正として,力のつり合いの式を立てるとこうね。
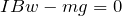
そうだね。そもそも図の中に

という文字がないもんね。実は,図の中の文字でいうと,電流
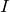
は与えられていないんだよね。
それじゃあ,まず電流を求めなきゃダメね。どうすればいい?
そういえば,そうだったわね。こうね。
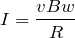
そうだったよね。さっきのつり合いの式と合わせて,

を求めよう。
あとは簡単ね。つり合いの式に今の
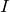
を代入するわね。
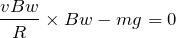
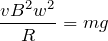
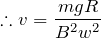



![]() という文字が入っていたり,いやな感じではあるよね。一応この式を使っても答えは出せるんだけど,この式から導き出される次の式の方が使いやすいんだ。
という文字が入っていたり,いやな感じではあるよね。一応この式を使っても答えは出せるんだけど,この式から導き出される次の式の方が使いやすいんだ。

![]() を求めることになっているよ。
を求めることになっているよ。![]() とすると,さっきの式
とすると,さっきの式![]() が使えるのね。
が使えるのね。
![]() は,
は,
![]()
![]() だから,流れる電流
だから,流れる電流![]() はどうなるかな?
はどうなるかな?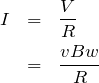










![]() で電流が0になるのか,そのまま電流が流れ続けるのか,という2択ね。
で電流が0になるのか,そのまま電流が流れ続けるのか,という2択ね。![]() はコイルがすべて磁場に入った時だよね。
はコイルがすべて磁場に入った時だよね。
![]() だから,逆向きで打ち消し合うということね。
だから,逆向きで打ち消し合うということね。
![]() 」を求める問題ね。等速だから,速さ=距離÷時間よね。つまり,
」を求める問題ね。等速だから,速さ=距離÷時間よね。つまり,![]() から
から![]() の間に
の間に![]() だけ落下するから,こうね。
だけ落下するから,こうね。
![]()
![]() か
か![]() を他の文字で表せばいいわよね。
を他の文字で表せばいいわよね。





![]() の導線を流れる電流
の導線を流れる電流![]() が磁束密度Bの磁場から受ける力の大きさ
が磁束密度Bの磁場から受ける力の大きさ![]() は,こう表せるんだ。
は,こう表せるんだ。
![]() ,
,![]() ,
,![]() はそれぞれ垂直の関係だからね。垂直じゃない場合は,垂直な成分を考えることになるよ。
はそれぞれ垂直の関係だからね。垂直じゃない場合は,垂直な成分を考えることになるよ。
![]() ,
,![]() ,
,![]() がすべて同じだから,はたらく力の大きさ
がすべて同じだから,はたらく力の大きさ![]() も同じなので,力がつり合っているんだね。
も同じなので,力がつり合っているんだね。![]() だからこんな感じね。
だからこんな感じね。
![]() だけど,鉛直方向の力のつり合いの式を立てても
だけど,鉛直方向の力のつり合いの式を立てても![]() は出てきそうもないわ。一応鉛直上向きを正として,力のつり合いの式を立てるとこうね。
は出てきそうもないわ。一応鉛直上向きを正として,力のつり合いの式を立てるとこうね。![]()
![]() という文字がないもんね。実は,図の中の文字でいうと,電流
という文字がないもんね。実は,図の中の文字でいうと,電流![]() は与えられていないんだよね。
は与えられていないんだよね。![]()
![]() を求めよう。
を求めよう。![]() を代入するわね。
を代入するわね。![]()
![]()
![]()