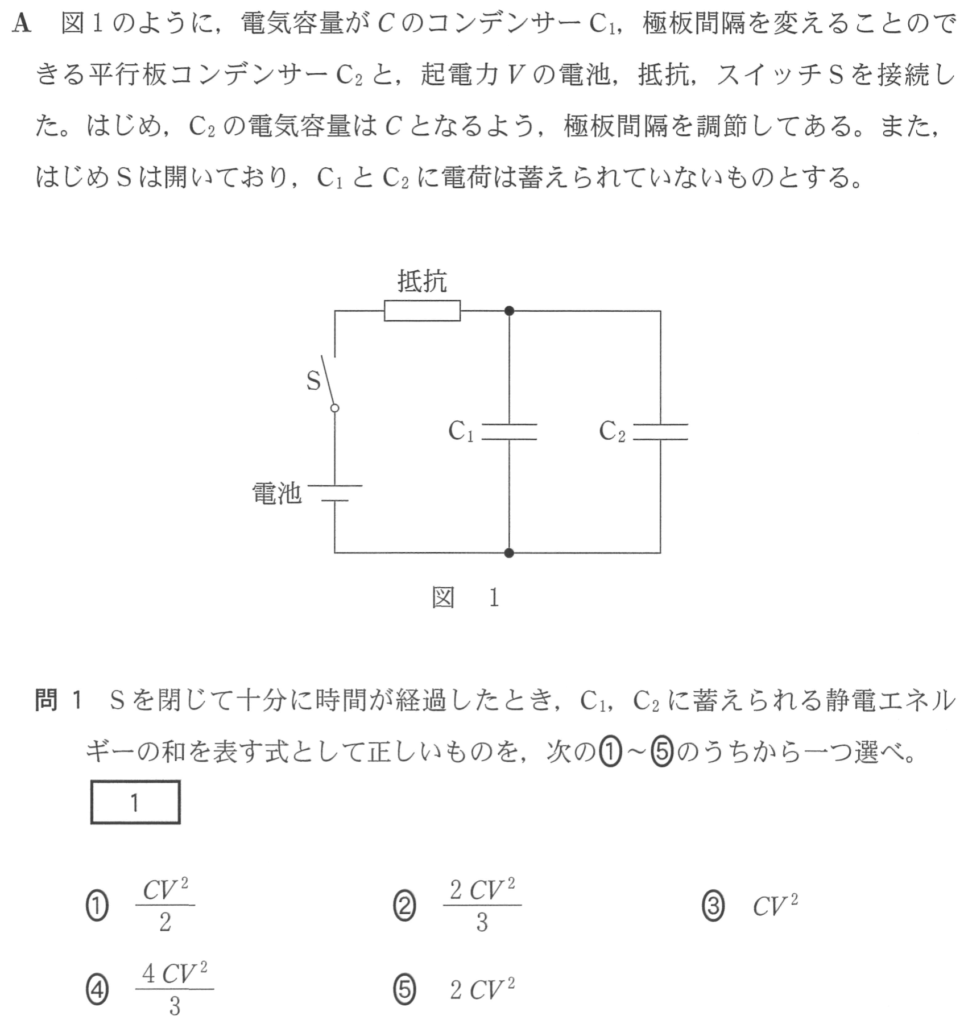
静電エネルギーの3つの式を使い分けよう
物理が苦手な文子
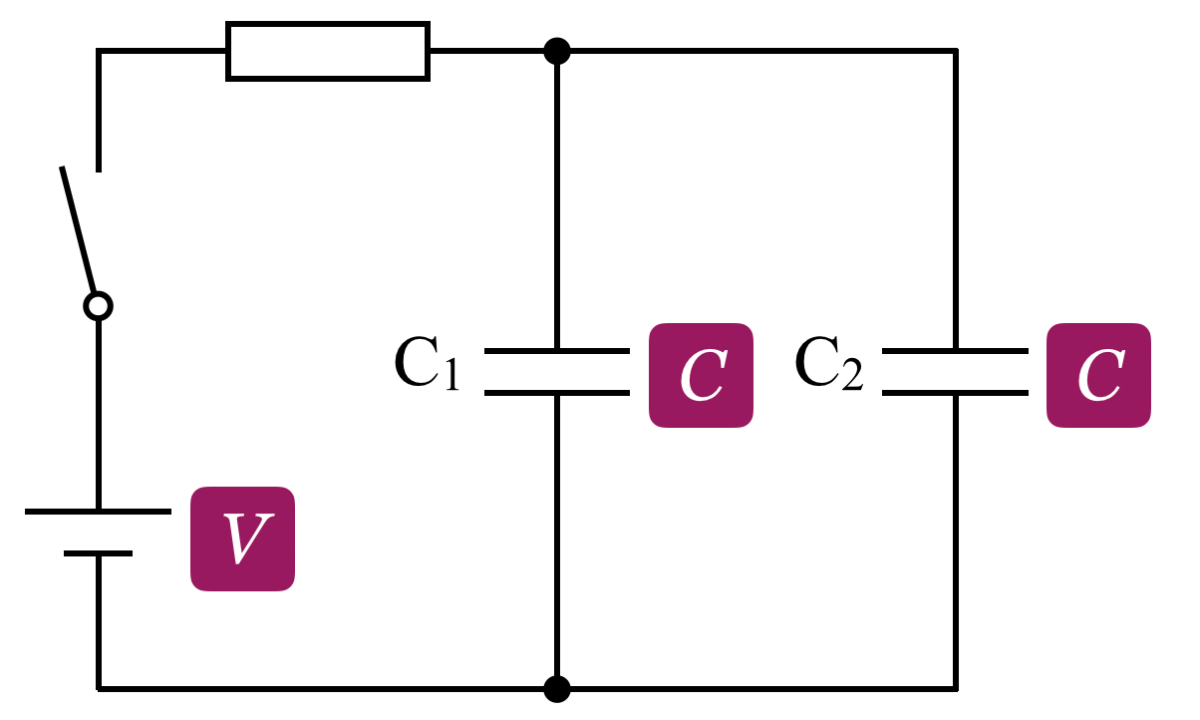
スイッチSを閉じて十分時間が経つと,2つのコンデンサーの両端の電圧は電池の起電力 になるのよね。
になるのよね。
物理が得意な秀樹
そうだね。コンデンサーに蓄えられる静電エネルギーの式を確認しておこう。

物理が苦手な文子
最初はコンデンサーC2の電気容量が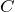 だから,使うのは
だから,使うのは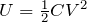 ね。
ね。
物理が得意な秀樹
求めたいのは静電エネルギーの和だね。
物理が苦手な文子
こういうことね。
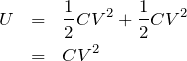
物理が得意な秀樹
そう,答えは③だ。
電気容量は極板間隔に反比例する
物理が苦手な文子
最初の空欄は,極板間隔を2倍にすると,電気容量がどうなるかね。
物理が得意な秀樹
この電気容量の関係式は覚えてるよね。

物理が苦手な文子
覚えているわ。電気容量は極板間隔に反比例するから,最初の空欄は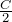 ね。
ね。
物理が得意な秀樹
そうだね。
物理が苦手な文子
次は並列の合成容量ね。並列の場合は単純に電気容量の和を取ればいいのよね。
直列の合成容量の式には注意が必要
物理が得意な秀樹
並列の場合は,それで問題ないね。一応確認しておくけど,直列の場合の合成容量の式はコンデンサーに蓄えられている電気量が同じじゃないと使えないからね。

物理が苦手な文子
えっ,そうなの?知らなかった。ちゃんと覚えておくわ。今は並列だから,合成容量を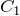 とすると,
とすると,
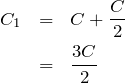
物理が得意な秀樹
これで答えが③か④に絞られたね。
電圧を求めるために,電気量保存の式を立てる
物理が苦手な文子
最後の空欄は電圧を求めるんだけど,これはどうすればいいの?
物理が得意な秀樹
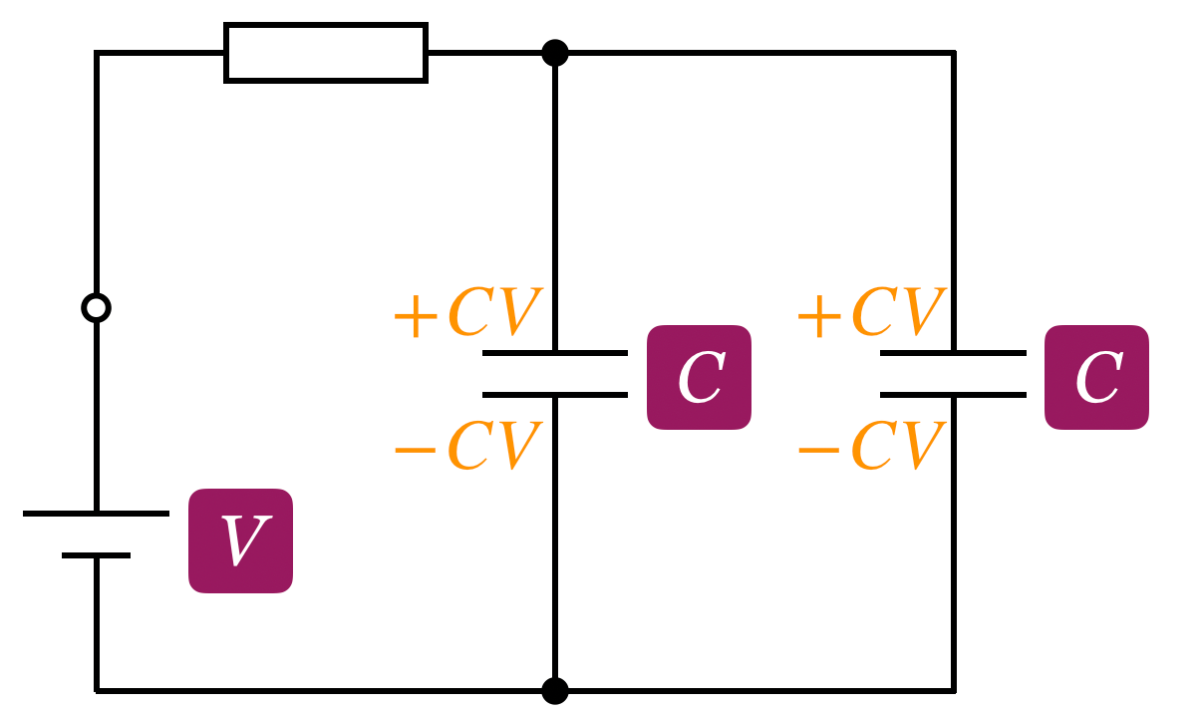
まずはスイッチを開く前の電気量を確認しておこう。
物理が苦手な文子
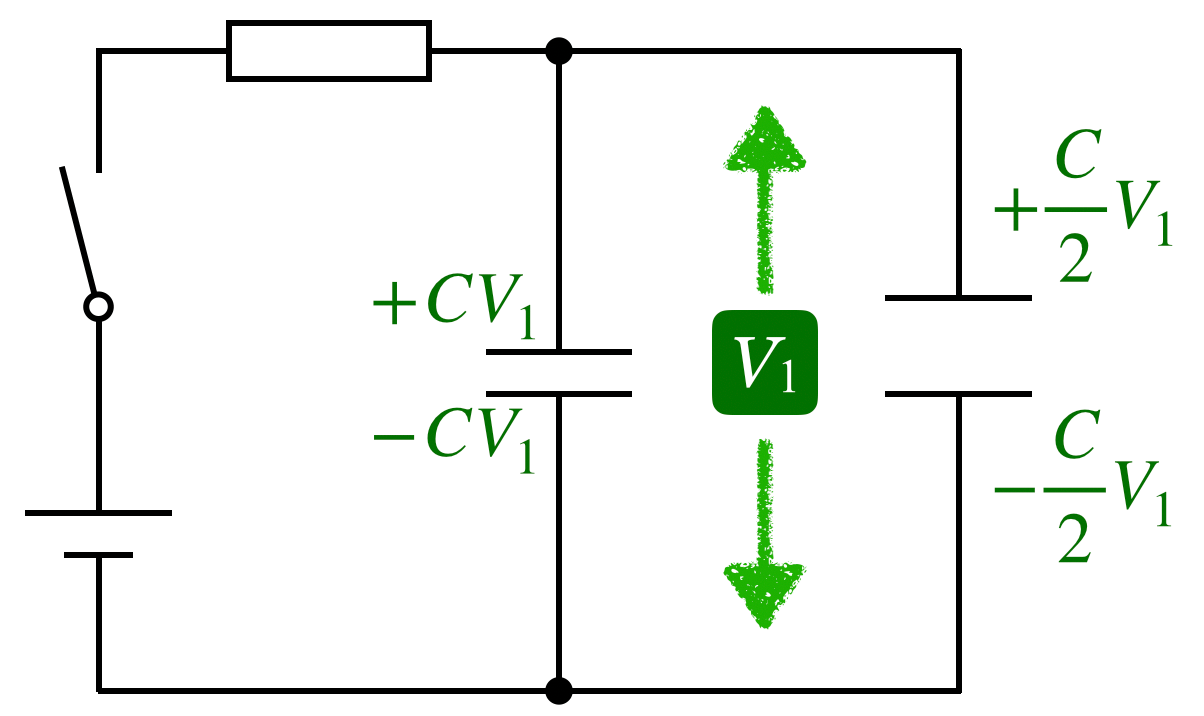
電気量はこんな感じね。
物理が得意な秀樹
スイッチを開いてから極板間隔を2倍にするんだよね。
物理が苦手な文子
その時の電圧を求めるんだから,電圧を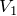 ,電気量をそれぞれ
,電気量をそれぞれ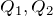 として
として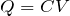 の式を2本立てて連立方程式を解けばいいわね。
の式を2本立てて連立方程式を解けばいいわね。
物理が得意な秀樹
あと電気量保存の式も必要だね。3本の連立方程式だ。もちろんそれでもいいけど,連立しないで解く方法も知っているといいよ。求める電圧を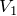 とするところまでは同じだ。
とするところまでは同じだ。
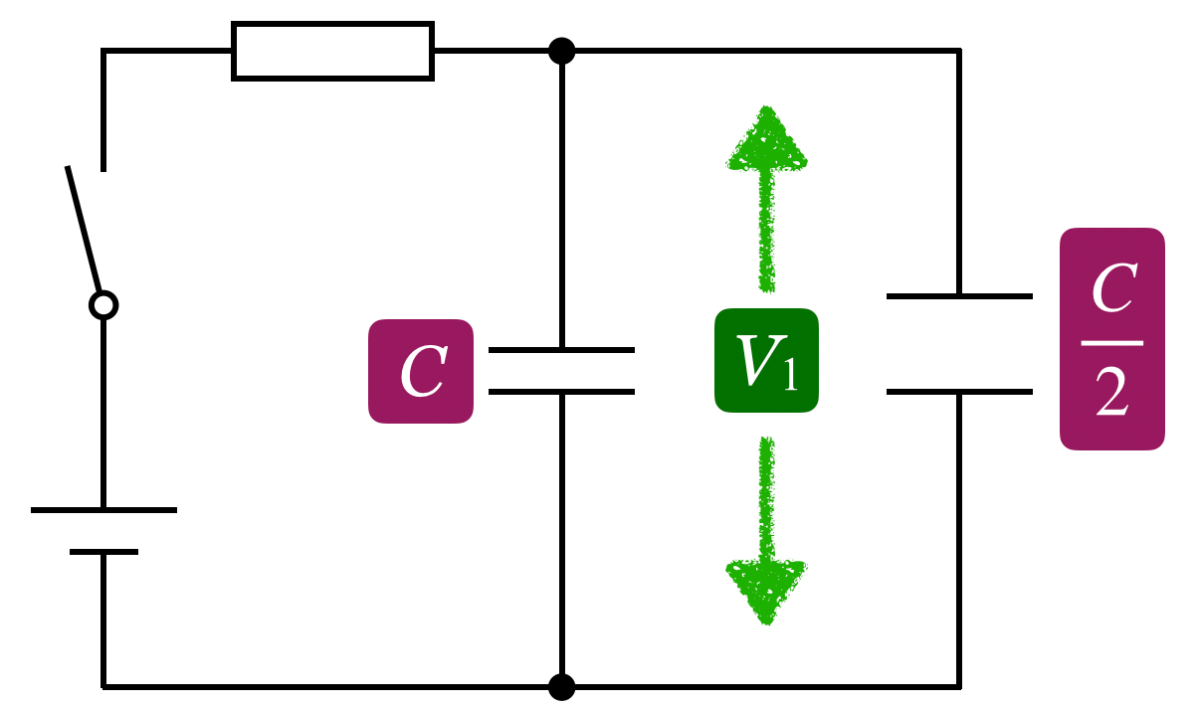
物理が得意な秀樹
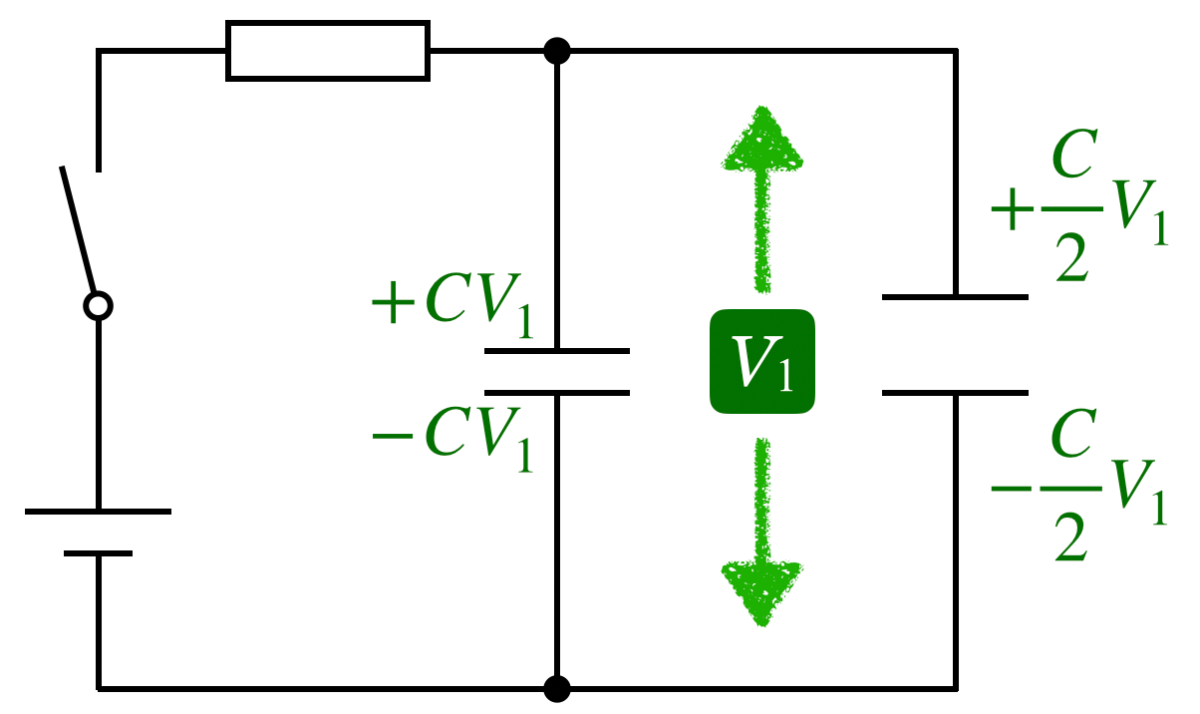
2つのコンデンサーに蓄えられる電気量を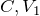 で表してみよう。
で表してみよう。
物理が苦手な文子
それは簡単。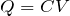 を使うえばいいわね。
を使うえばいいわね。
物理が得意な秀樹
あとは電気量保存の式を立てるだけだ。
物理が苦手な文子
えっ,それだけ。スイッチを開く前と開いたあとで電気量保存の式を立てるわね。
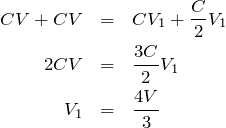
物理が得意な秀樹
簡単だったでしょ。答えは④だ。