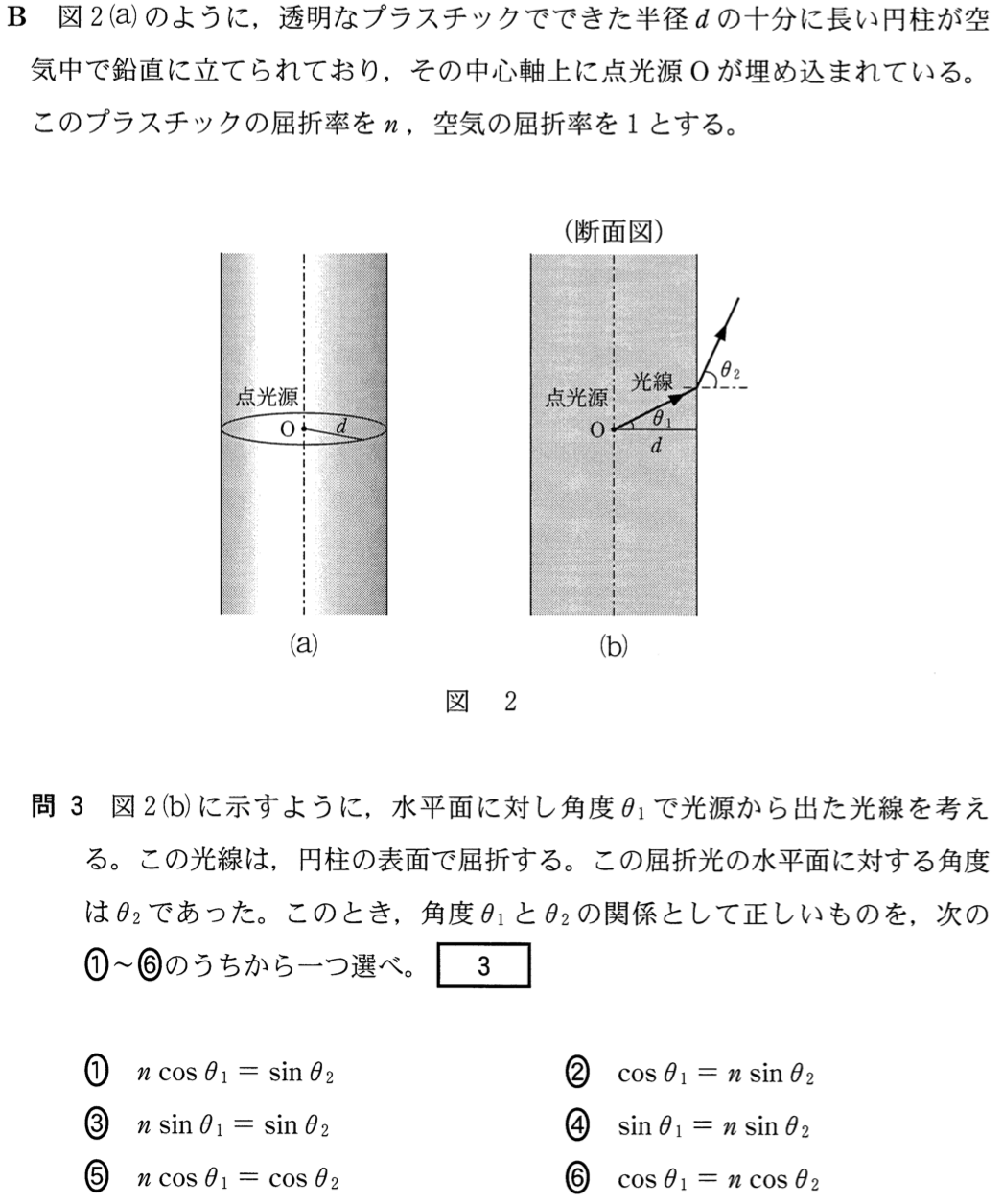
物理が苦手な文子
屈折の問題ね。割と好きなんだけど、この問題は境界線が縦になっているから少し分かりにくいわ。
物理が得意な秀樹
そうだね。そういうときは、問題を横にしてみたら?
物理が苦手な文子
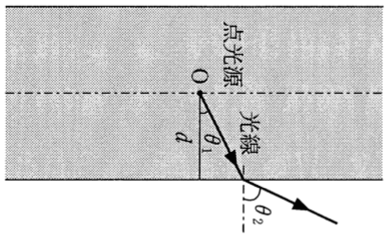
確かに見慣れた図になったわ。文字が横になっちゃうけど。
物理が得意な秀樹
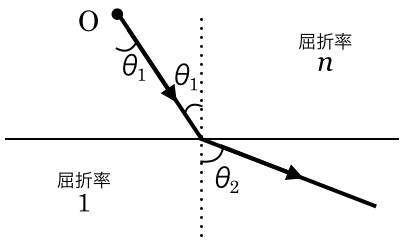
横にした図を描いちゃってもいいかもね。
物理が苦手な文子
ものすごく分かりやすくなったわ。私が覚えている屈折の法則は、分数の形なので、
![]()
![]()
物理が苦手な文子
これでいいかな?
物理が得意な秀樹
そうだね。答えは③だ。次は問4だね。
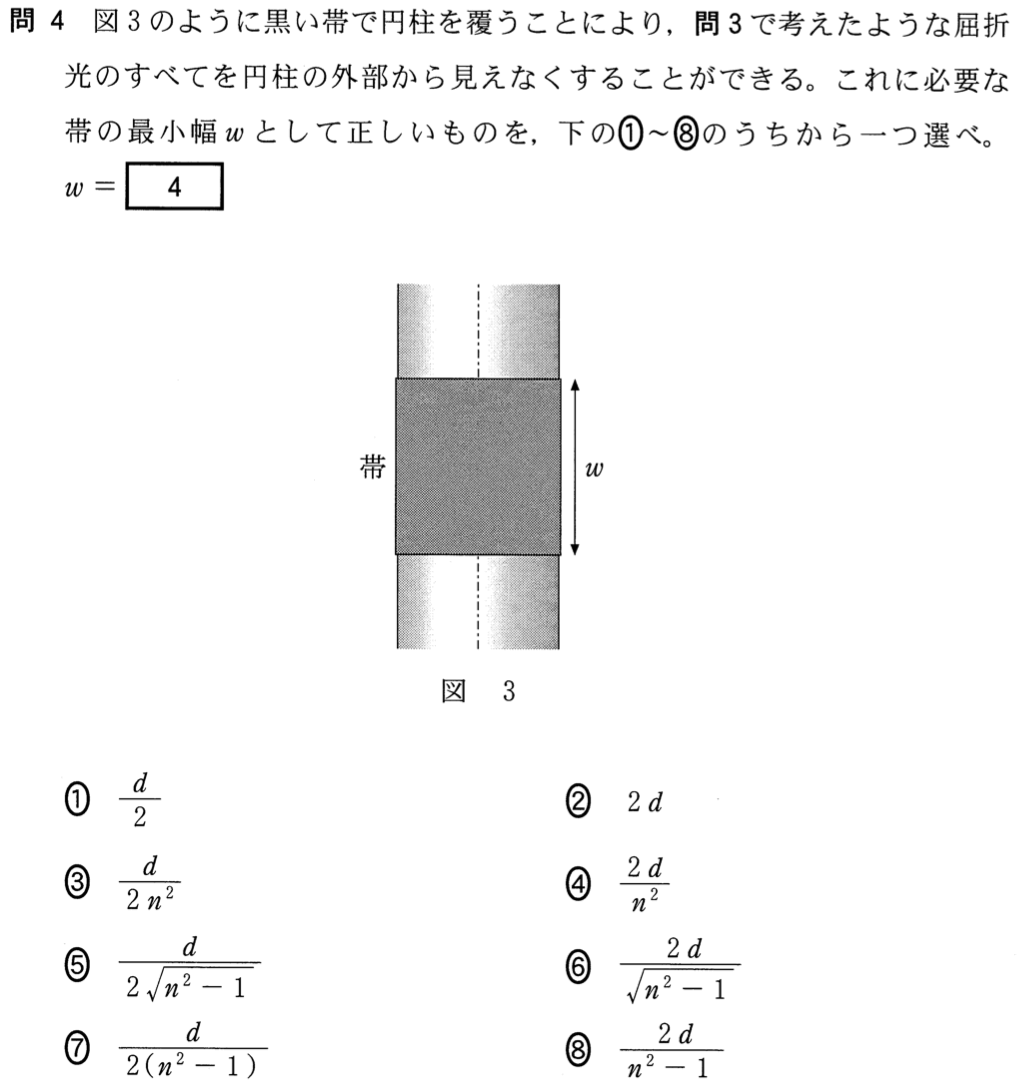
物理が苦手な文子
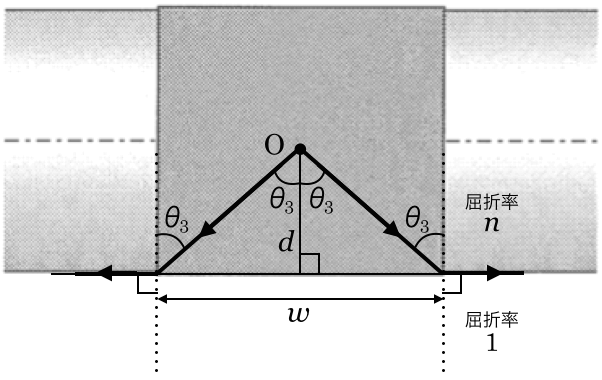
外部から見えなくするっていう問題も見たことがあるわ。最小幅を求める問題だから、臨界角を求める問題と同じよね。だけどまた図が縦なのよね。
物理が得意な秀樹
図を横にして、さらにいろいろと描き込んでみるよ。
物理が苦手な文子
すごく分かりやすいわ。臨界角を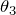 として、描いたのね。それと、臨界角のときだから屈折角を90°にしてしてあるのね。
として、描いたのね。それと、臨界角のときだから屈折角を90°にしてしてあるのね。
物理が得意な秀樹
じゃあ、屈折の法則を使ってみようか。
物理が苦手な文子
この図があれば、あとは計算ね。
![]()
![]()
物理が得意な秀樹
ここまでは問3と同じだね。あとはどうしよう。
物理が苦手な文子
右側の直角三角形から、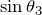 を求めればいいのよね。まず、斜辺を
を求めればいいのよね。まず、斜辺を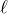 として斜辺を求めるわ。
として斜辺を求めるわ。
![]()
![]()
物理が得意な秀樹
それから?
物理が苦手な文子
直角三角形で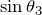 を表すわよ。
を表すわよ。
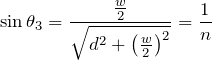
![]()
物理が苦手な文子
両辺平方して、
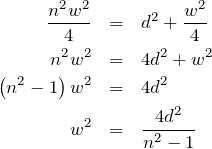
物理が苦手な文子
![]()
物理が苦手な文子
ふぅ、できた!
物理が得意な秀樹
正解!答えは⑥だ!