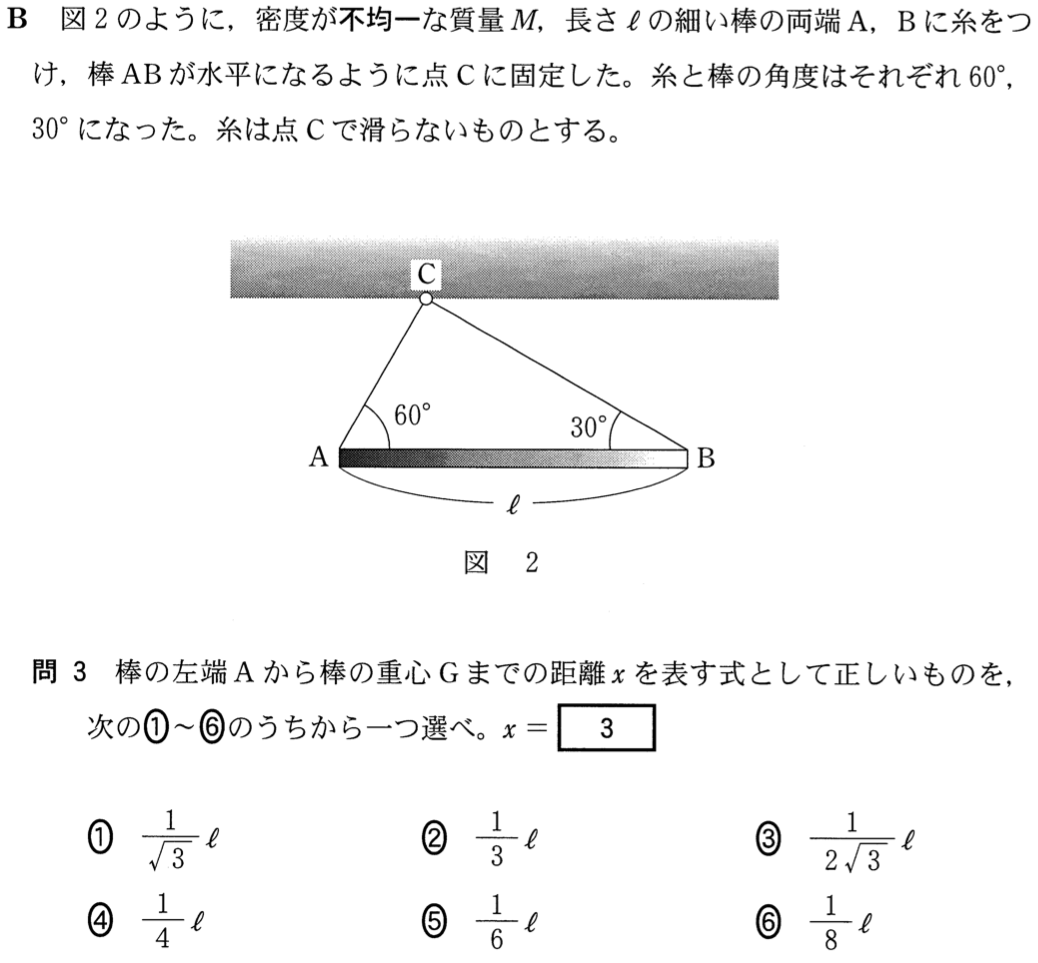
そうなんだけど、まぁちょっといろいろあるので、やってみよう!
ちょっと待って!「力の矢印を描く」というは、正しい進め方なんだけど、今回はちょっと後にしてみない?他になんかできそうなことがないかな?
そういえば、重心を求める公式ってあったような気がする。でもあの公式って、よく分からないんだよね。
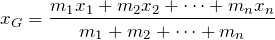
この式を覚えていなくても当然で、この式を使わなくても重心の位置って求められるんだよね。
そうなのよ。この式を使わなくても問題が解けるのよ。
だから、この問題もこの式を使わなくても解けるんだよ。
力の矢印も描かないし、公式も使わないの?どうするの?
さっき紹介した
「重心」っていうサイトにも「吊すと分かる」って書いてあるじゃない?「剛体の1点を糸で吊るして静止したとき、重心は糸の張力の作用線上にきます。」と書いてあるね。この問題は棒と糸はAとBの2点で繋がっているけど、天井とはC1点だけで吊しているので、天井が糸を引く力の作用線上に棒の重心はあるんだ。
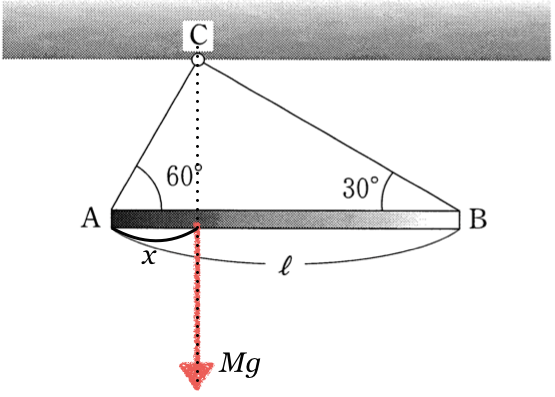
へぇ〜そういうことなんだ。ちょっと気がつかないかな。
気がつかなくても、力の矢印をきちんと描けば答えはでるので、その方法もやってみてね。それではこの図から

を求めてみよう。
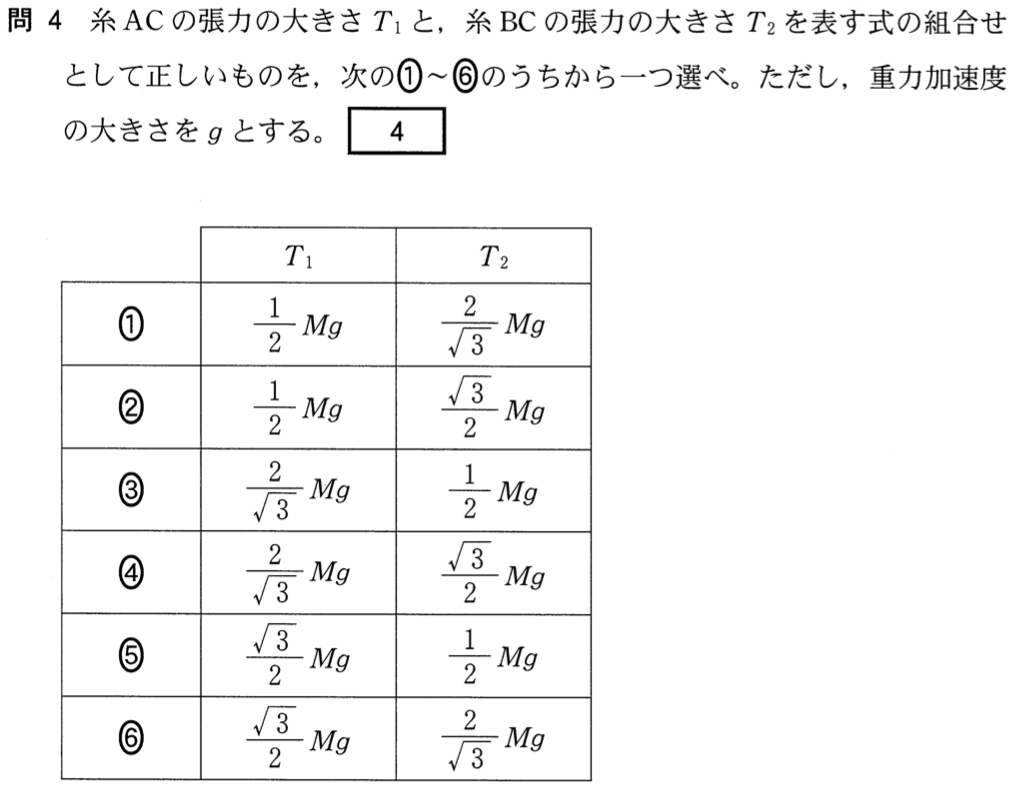
選択肢を見ると、

を
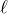
で表せばいいのね。直角三角形から求めることができそうね。とりあえず、左側の直角三角形から、ACは
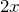
ね。
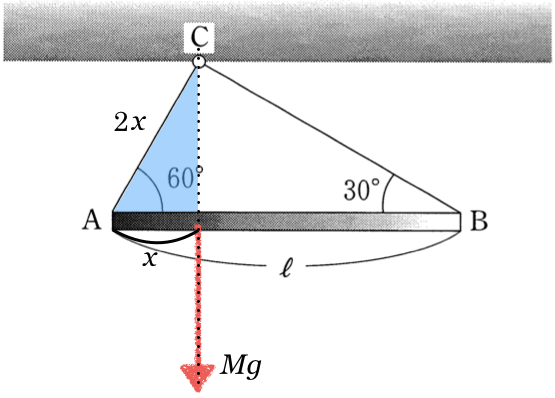
それじゃあ、直角三角形ABCを考えると、ABは
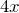
になるわね。
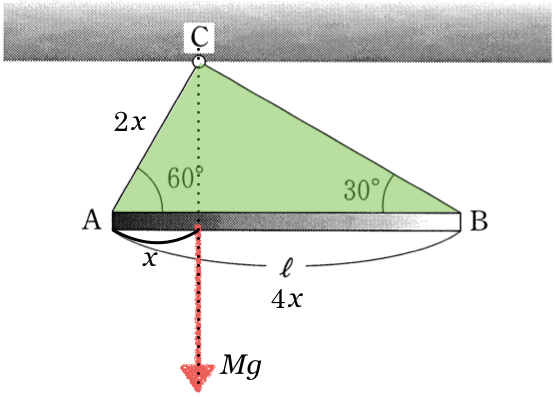
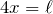
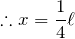
いよいよ、力のモーメントのつり合いね。さすがに力の矢印を描かなきゃダメでしょ?
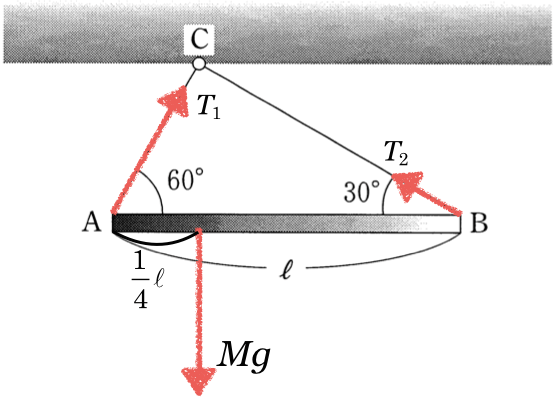
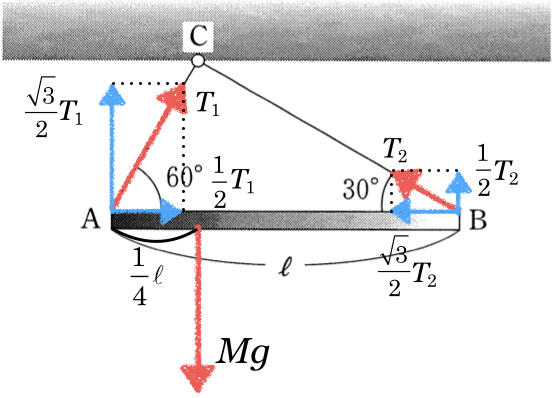
水平方向と、鉛直方向の力のつり合いと、力のモーメントのつり合いの3本の式を書くのね。
すばらしい!通常はそう考えるんだけど、今は
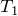
と
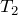
以外に不明な文字はないから、力のつり合いの式だけで大丈夫だよ。
そうなの?まぁやってみるわ。水平方向は右向きを正として、
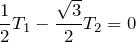
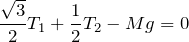
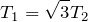
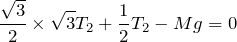
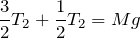
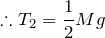
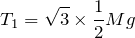

![]()

![]() を求めてみよう。
を求めてみよう。![]()
![]()
![]() と
と![]() 以外に不明な文字はないから、力のつり合いの式だけで大丈夫だよ。
以外に不明な文字はないから、力のつり合いの式だけで大丈夫だよ。![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 センター試験の問題で「物理」を学ぼう!
センター試験の問題で「物理」を学ぼう!![]()

![]() を求めてみよう。
を求めてみよう。![]()
![]()
![]() と
と![]() 以外に不明な文字はないから、力のつり合いの式だけで大丈夫だよ。
以外に不明な文字はないから、力のつり合いの式だけで大丈夫だよ。![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()